Question Number 89237 by cindiaulia last updated on 16/Apr/20
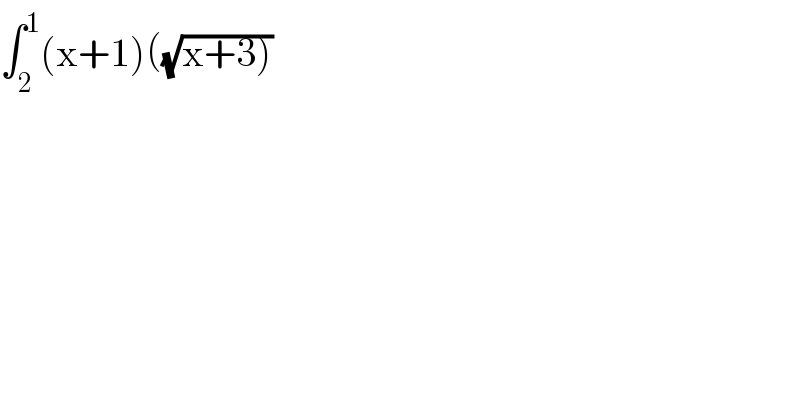
$$\int_{\mathrm{2}} ^{\mathrm{1}} \left(\mathrm{x}+\mathrm{1}\right)\left(\sqrt{\left.\mathrm{x}+\mathrm{3}\right)}\right. \\ $$
Commented by niroj last updated on 16/Apr/20
![= ∫_2 ^1 (x+1)(√(x+3)) dx put(√(x+3)) = t x+3=t^2 ⇒ x=t^2 −3 dx= 2tdt if x=1⇒ t=2 if x=2⇒ t=(√5) ∫_(√5) ^( 2) (t^2 −3+1) t.2tdt = ∫_(√5) ^2 (t^2 −2)2t^2 dt = ∫_(√5) ^2 (2t^4 −4t^2 )dt = [ 2∫t^4 dt−4∫t^2 dt]_(√5) ^2 = [2.(t^5 /5)−4.(t^3 /3)]_(√5) ^2 = [(2/5)t^5 −(4/3)t^3 ]_(√5) ^2 = [(2/5)(2)^5 −(4/3)2^3 ]−[(2/5)((√5) )^5 −(4/3)((√5))^3 ] =( ((2.32)/5)−((4.8)/3))−((2/5).25(√5) −(4/3).5(√5) ) = ((64)/5)−((32)/3)− 10(√5) +((20(√5))/3) = ((64)/5)−((32)/3)−(((30(√5) −20(√5))/3) ) = ((64)/5)−((32)/3)−((10(√5))/3) //. = 12.8−10.67−7.453 =4.677 //.](https://www.tinkutara.com/question/Q89265.png)
$$=\:\int_{\mathrm{2}} ^{\mathrm{1}} \left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{x}+\mathrm{3}}\:\:\mathrm{dx} \\ $$$$\:\:\:\mathrm{put}\sqrt{\mathrm{x}+\mathrm{3}}\:\:=\:\mathrm{t} \\ $$$$\:\:\:\:\:\:\mathrm{x}+\mathrm{3}=\mathrm{t}^{\mathrm{2}} \:\:\Rightarrow\:\:\:\mathrm{x}=\mathrm{t}^{\mathrm{2}} −\mathrm{3} \\ $$$$\:\:\:\:\:\mathrm{dx}=\:\mathrm{2tdt} \\ $$$$\:\:\:\:\:\:\:\mathrm{if}\:\mathrm{x}=\mathrm{1}\Rightarrow\:\mathrm{t}=\mathrm{2} \\ $$$$\:\:\:\:\:\:\mathrm{if}\:\mathrm{x}=\mathrm{2}\Rightarrow\:\mathrm{t}=\sqrt{\mathrm{5}} \\ $$$$\:\:\:\: \\ $$$$\:\:\int_{\sqrt{\mathrm{5}}} ^{\:\mathrm{2}} \:\left(\mathrm{t}^{\mathrm{2}} −\mathrm{3}+\mathrm{1}\right)\:\mathrm{t}.\mathrm{2tdt} \\ $$$$\:\:=\:\int_{\sqrt{\mathrm{5}}} ^{\mathrm{2}} \:\:\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2}\right)\mathrm{2t}^{\mathrm{2}} \mathrm{dt} \\ $$$$=\:\:\int_{\sqrt{\mathrm{5}}} ^{\mathrm{2}} \:\left(\mathrm{2t}^{\mathrm{4}} −\mathrm{4t}^{\mathrm{2}} \right)\mathrm{dt} \\ $$$$=\:\left[\:\mathrm{2}\int\mathrm{t}^{\mathrm{4}} \mathrm{dt}−\mathrm{4}\int\mathrm{t}^{\mathrm{2}} \mathrm{dt}\right]_{\sqrt{\mathrm{5}}} ^{\mathrm{2}} \\ $$$$\:=\:\left[\mathrm{2}.\frac{\mathrm{t}^{\mathrm{5}} }{\mathrm{5}}−\mathrm{4}.\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{3}}\right]_{\sqrt{\mathrm{5}}} ^{\mathrm{2}} =\:\left[\frac{\mathrm{2}}{\mathrm{5}}\mathrm{t}^{\mathrm{5}} −\frac{\mathrm{4}}{\mathrm{3}}\mathrm{t}^{\mathrm{3}} \right]_{\sqrt{\mathrm{5}}} ^{\mathrm{2}} \\ $$$$=\:\left[\frac{\mathrm{2}}{\mathrm{5}}\left(\mathrm{2}\right)^{\mathrm{5}} −\frac{\mathrm{4}}{\mathrm{3}}\mathrm{2}^{\mathrm{3}} \right]−\left[\frac{\mathrm{2}}{\mathrm{5}}\left(\sqrt{\mathrm{5}}\:\right)^{\mathrm{5}} −\frac{\mathrm{4}}{\mathrm{3}}\left(\sqrt{\mathrm{5}}\right)^{\mathrm{3}} \right] \\ $$$$=\left(\:\frac{\mathrm{2}.\mathrm{32}}{\mathrm{5}}−\frac{\mathrm{4}.\mathrm{8}}{\mathrm{3}}\right)−\left(\frac{\mathrm{2}}{\mathrm{5}}.\mathrm{25}\sqrt{\mathrm{5}}\:−\frac{\mathrm{4}}{\mathrm{3}}.\mathrm{5}\sqrt{\mathrm{5}}\:\right) \\ $$$$=\:\frac{\mathrm{64}}{\mathrm{5}}−\frac{\mathrm{32}}{\mathrm{3}}−\:\mathrm{10}\sqrt{\mathrm{5}}\:+\frac{\mathrm{20}\sqrt{\mathrm{5}}}{\mathrm{3}} \\ $$$$=\:\frac{\mathrm{64}}{\mathrm{5}}−\frac{\mathrm{32}}{\mathrm{3}}−\left(\frac{\mathrm{30}\sqrt{\mathrm{5}}\:\:−\mathrm{20}\sqrt{\mathrm{5}}}{\mathrm{3}}\:\right) \\ $$$$=\:\frac{\mathrm{64}}{\mathrm{5}}−\frac{\mathrm{32}}{\mathrm{3}}−\frac{\mathrm{10}\sqrt{\mathrm{5}}}{\mathrm{3}}\://. \\ $$$$=\:\mathrm{12}.\mathrm{8}−\mathrm{10}.\mathrm{67}−\mathrm{7}.\mathrm{453} \\ $$$$=\mathrm{4}.\mathrm{677}\://. \\ $$$$\:\:\: \\ $$$$\:\: \\ $$
