Question Number 78766 by M±th+et£s last updated on 20/Jan/20
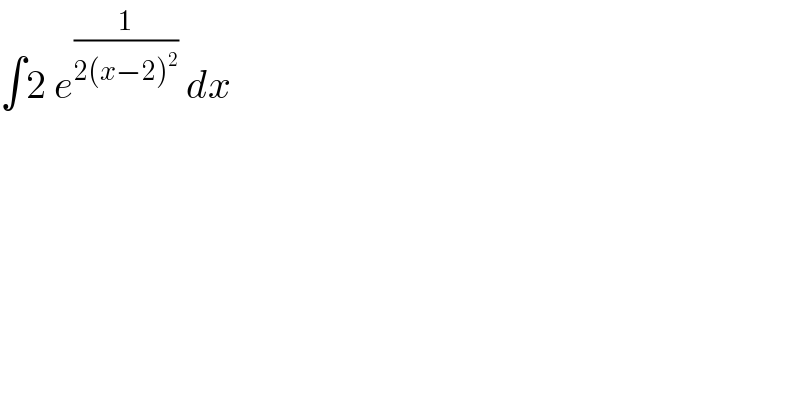
$$\int\mathrm{2}\:{e}^{\frac{\mathrm{1}}{\mathrm{2}\left({x}−\mathrm{2}\right)^{\mathrm{2}} }} \:{dx} \\ $$
Answered by MJS last updated on 20/Jan/20
![2∫e^(1/(2(x−2)^2 )) dx= [t=2−x → dx=−dt] =−2∫e^(1/(2t^2 )) dt= by parts: u′=1 → u=t v=e^(1/(2t^2 )) → v′=−(e^(1/(2t^2 )) /t^3 ) =−2te^(1/(2t^2 )) +2∫−(e^(1/(2t^2 )) /t^2 )dt= [u=(1/( (√2)t)) → dt=−(√2)t^2 du] =−2te^(1/(2t^2 )) +(√(2π))∫((2e^u^2 )/( (√π)))du= =−2te^(1/(2t^2 )) +(√(2π))erfi u = =−2te^(1/(2t^2 )) +(√(2π))erfi (1/( (√2)t))= =−2(2−x)e^(1/(2(2−x)^2 )) +(√(2π))erfi ((√2)/(2(2−x))) +C](https://www.tinkutara.com/question/Q78782.png)
$$\mathrm{2}\int\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}\left({x}−\mathrm{2}\right)^{\mathrm{2}} }} {dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{2}−{x}\:\rightarrow\:{dx}=−{dt}\right] \\ $$$$=−\mathrm{2}\int\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} }} {dt}= \\ $$$$\:\:\:\:\:\mathrm{by}\:\mathrm{parts}: \\ $$$$\:\:\:\:\:{u}'=\mathrm{1}\:\rightarrow\:{u}={t} \\ $$$$\:\:\:\:\:{v}=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} }} \:\rightarrow\:{v}'=−\frac{\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} }} }{{t}^{\mathrm{3}} } \\ $$$$=−\mathrm{2}{t}\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} }} +\mathrm{2}\int−\frac{\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} }} }{{t}^{\mathrm{2}} }{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}{t}}\:\rightarrow\:{dt}=−\sqrt{\mathrm{2}}{t}^{\mathrm{2}} {du}\right] \\ $$$$=−\mathrm{2}{t}\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} }} +\sqrt{\mathrm{2}\pi}\int\frac{\mathrm{2e}^{{u}^{\mathrm{2}} } }{\:\sqrt{\pi}}{du}= \\ $$$$=−\mathrm{2}{t}\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} }} +\sqrt{\mathrm{2}\pi}\mathrm{erfi}\:{u}\:= \\ $$$$=−\mathrm{2}{t}\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} }} +\sqrt{\mathrm{2}\pi}\mathrm{erfi}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}{t}}= \\ $$$$=−\mathrm{2}\left(\mathrm{2}−{x}\right)\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}−{x}\right)^{\mathrm{2}} }} +\sqrt{\mathrm{2}\pi}\mathrm{erfi}\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}\left(\mathrm{2}−{x}\right)}\:+{C} \\ $$
Commented by mind is power last updated on 20/Jan/20

$$\mathrm{Nice} \\ $$
Commented by M±th+et£s last updated on 20/Jan/20

$${thank}\:{you}\:{sir} \\ $$
