Question Number 40583 by Cheyboy last updated on 24/Jul/18

$$\mathrm{2}^{\sqrt{{x}}} =\:{x} \\ $$$${find}\:{x} \\ $$
Answered by $@ty@m last updated on 24/Jul/18

$$\mathrm{4} \\ $$
Commented by Cheyboy last updated on 24/Jul/18
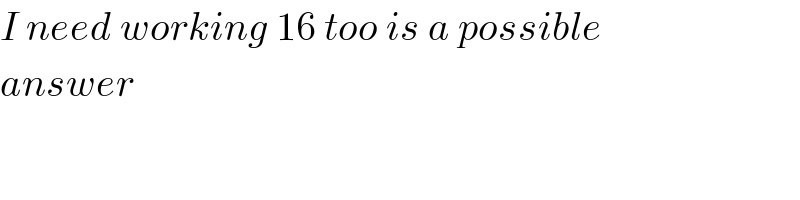
$${I}\:{need}\:{working}\:\mathrm{16}\:{too}\:{is}\:{a}\:{possible} \\ $$$${answer} \\ $$
Answered by MrW3 last updated on 24/Jul/18
![let t=(√x)>0 2^t =t^2 2^(t/2) =t e^((ln 2 t)/2) =t −((ln 2)/2)=−((ln 2 t)/2) e^(−((ln 2 t)/2)) ⇒−((ln 2 t)/2)=W(−((ln 2)/2)) ⇒t=−(2/(ln 2)) W(−((ln 2)/2)) ⇒x=t^2 =[−(2/(ln 2)) W(−((ln 2)/2))]^2 = { (((−((−2×1.3863)/(ln 2)))^2 =16)),(((−((−2×0.6931)/(ln 2)))^2 =4)) :}](https://www.tinkutara.com/question/Q40586.png)
$${let}\:{t}=\sqrt{{x}}>\mathrm{0} \\ $$$$\mathrm{2}^{{t}} ={t}^{\mathrm{2}} \\ $$$$\mathrm{2}^{\frac{{t}}{\mathrm{2}}} ={t} \\ $$$${e}^{\frac{\mathrm{ln}\:\mathrm{2}\:{t}}{\mathrm{2}}} ={t} \\ $$$$−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}=−\frac{\mathrm{ln}\:\mathrm{2}\:{t}}{\mathrm{2}}\:{e}^{−\frac{\mathrm{ln}\:\mathrm{2}\:{t}}{\mathrm{2}}} \\ $$$$\Rightarrow−\frac{\mathrm{ln}\:\mathrm{2}\:{t}}{\mathrm{2}}={W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right) \\ $$$$\Rightarrow{t}=−\frac{\mathrm{2}}{\mathrm{ln}\:\mathrm{2}}\:{W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right) \\ $$$$\Rightarrow{x}={t}^{\mathrm{2}} =\left[−\frac{\mathrm{2}}{\mathrm{ln}\:\mathrm{2}}\:{W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right)\right]^{\mathrm{2}} =\begin{cases}{\left(−\frac{−\mathrm{2}×\mathrm{1}.\mathrm{3863}}{\mathrm{ln}\:\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{16}}\\{\left(−\frac{−\mathrm{2}×\mathrm{0}.\mathrm{6931}}{\mathrm{ln}\:\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{4}}\end{cases} \\ $$
Commented by Cheyboy last updated on 24/Jul/18

$${Thank}\:{you}\:{sir}!!\:{Really}\:{appreciated} \\ $$
Commented by MrW3 last updated on 24/Jul/18

$${You}\:{are}\:{welcome}\:{sir}! \\ $$$${what}\:{if}\:{the}\:{question}\:{is}: \\ $$$$\mathrm{2}^{{x}} ={x}^{\mathrm{2}} \\ $$$${find}\:{x}. \\ $$
Commented by Cheyboy last updated on 25/Jul/18

$$\:\:\:{x}^{\mathrm{2}} \:=\:\mathrm{2}^{{x}} \\ $$$$\sqrt{{x}^{\mathrm{2}} }\:=\:\sqrt{\mathrm{2}^{{x}} } \\ $$$$\:{x}\:=\:\pm\:\mathrm{2}^{\frac{{x}}{\mathrm{2}}} \\ $$$$\:{x}\:=\:\pm\:{e}^{\frac{{x}}{\mathrm{2}}\mathrm{ln2}\:} \\ $$$$ \\ $$$$\:{xe}^{−\frac{{x}}{\mathrm{2}}\mathrm{ln2}} =\:\pm\:\mathrm{1} \\ $$$$ \\ $$$$−\frac{{x}}{\mathrm{2}}\mathrm{ln2}\:{e}^{−\:\frac{{x}}{\mathrm{2}}\mathrm{ln2}} \:=\:−\left(\pm\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right) \\ $$$$ \\ $$$${x}\:=\:−\frac{\mathrm{2}}{\mathrm{ln}\:\mathrm{2}}{W}\left(\pm\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right) \\ $$$$ \\ $$$${Sir}\:{i}\:{can}^{'} {t}\:{compute}\:{further} \\ $$$${No}\:{calculator}.. \\ $$$${Plzz}\:{verify} \\ $$$$ \\ $$
Commented by MrW3 last updated on 25/Jul/18

$${absolutely}\:{correct}! \\ $$$${W}\left(\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right)\:{has}\:{one}\:{value}\:\left(\mathrm{0}.\mathrm{2657}\right), \\ $$$${W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right)\:{has}\:{two}\:{values}\:\left({see}\:{above}\right), \\ $$$${so}\:{totally}\:{there}\:{are}\:{three}\:{solutions}\: \\ $$$${for}\:{x}. \\ $$
Commented by Cheyboy last updated on 26/Jul/18

$${Thank}\:{you}\:{sir}..\:{I}\:{wish}\:{you}\:{could}\: \\ $$$${teach}\:{maths}\:{an}\:{physics}.\:{I}\:{do} \\ $$$${learn}\:{a}\:{lot}\:{from}\:{answer},\:{and} \\ $$$${others}.. \\ $$
