Question Number 123256 by ZiYangLee last updated on 24/Nov/20
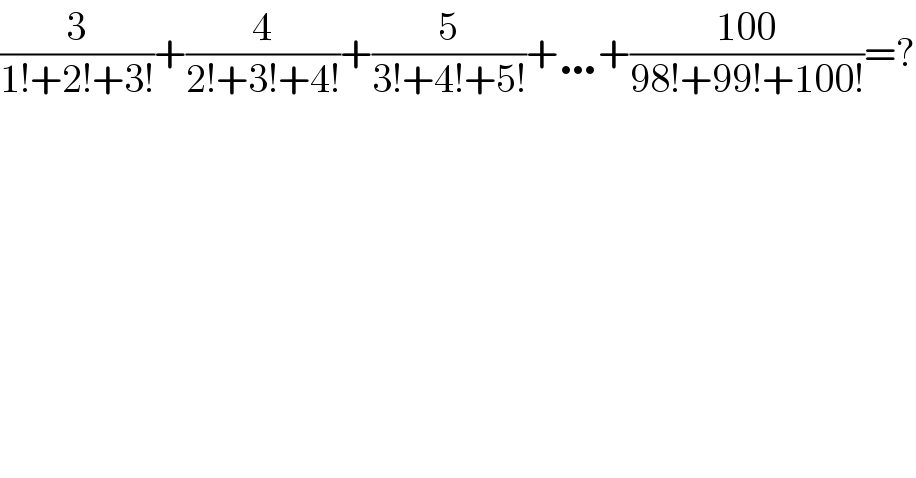
$$\frac{\mathrm{3}}{\mathrm{1}!+\mathrm{2}!+\mathrm{3}!}+\frac{\mathrm{4}}{\mathrm{2}!+\mathrm{3}!+\mathrm{4}!}+\frac{\mathrm{5}}{\mathrm{3}!+\mathrm{4}!+\mathrm{5}!}+\ldots+\frac{\mathrm{100}}{\mathrm{98}!+\mathrm{99}!+\mathrm{100}!}=? \\ $$
Commented by ZiYangLee last updated on 24/Nov/20
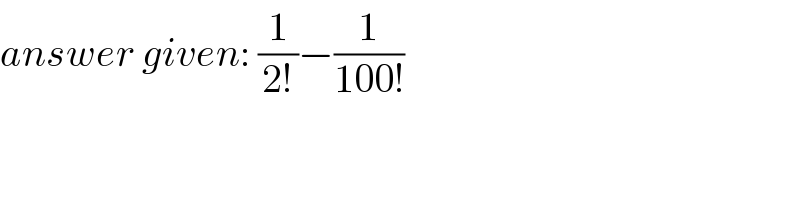
$${answer}\:{given}:\:\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{100}!} \\ $$
Commented by zarminaawan last updated on 24/Nov/20

$${how}\:{i}\:{upload}\:{my}\:{questios}\:{plzztell}\:{me}? \\ $$
Commented by Ar Brandon last updated on 24/Nov/20
Commented by Ar Brandon last updated on 24/Nov/20
While on forum tap there.
Answered by Olaf last updated on 24/Nov/20
![S = Σ_(n=3) ^(100) (n/((n−2)!+(n−1)(n−2)!+n(n−1)(n−2)!)) S = Σ_(n=3) ^(100) (n/((n−2)![1+(n−1)+n(n−1)])) S = Σ_(n=3) ^(100) (n/((n−2)!n^2 )) = Σ_(n=3) ^(100) (1/((n−2)!n)) S = Σ_(n=3) ^(100) ((n−1)/(n!)) = Σ_(n=3) ^(100) ((n/(n!))−(1/(n!))) = Σ_(n=3) ^(100) ((1/((n−1)!))−(1/(n!))) S = (1/(2!))−(1/(100!))](https://www.tinkutara.com/question/Q123297.png)
$$\mathrm{S}\:=\:\underset{{n}=\mathrm{3}} {\overset{\mathrm{100}} {\sum}}\frac{{n}}{\left({n}−\mathrm{2}\right)!+\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)!+{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)!} \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{3}} {\overset{\mathrm{100}} {\sum}}\frac{{n}}{\left({n}−\mathrm{2}\right)!\left[\mathrm{1}+\left({n}−\mathrm{1}\right)+{n}\left({n}−\mathrm{1}\right)\right]} \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{3}} {\overset{\mathrm{100}} {\sum}}\frac{{n}}{\left({n}−\mathrm{2}\right)!{n}^{\mathrm{2}} }\:=\:\underset{{n}=\mathrm{3}} {\overset{\mathrm{100}} {\sum}}\frac{\mathrm{1}}{\left({n}−\mathrm{2}\right)!{n}} \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{3}} {\overset{\mathrm{100}} {\sum}}\frac{{n}−\mathrm{1}}{{n}!}\:=\:\underset{{n}=\mathrm{3}} {\overset{\mathrm{100}} {\sum}}\left(\frac{{n}}{{n}!}−\frac{\mathrm{1}}{{n}!}\right)\:=\:\underset{{n}=\mathrm{3}} {\overset{\mathrm{100}} {\sum}}\left(\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!}−\frac{\mathrm{1}}{{n}!}\right) \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{100}!} \\ $$
Answered by MJS_new last updated on 24/Nov/20
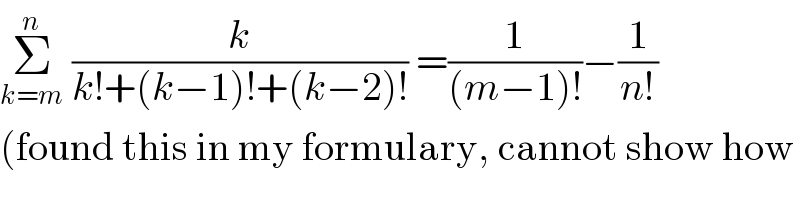
$$\underset{{k}={m}} {\overset{{n}} {\sum}}\:\frac{{k}}{{k}!+\left({k}−\mathrm{1}\right)!+\left({k}−\mathrm{2}\right)!}\:=\frac{\mathrm{1}}{\left({m}−\mathrm{1}\right)!}−\frac{\mathrm{1}}{{n}!} \\ $$$$\left(\mathrm{found}\:\mathrm{this}\:\mathrm{in}\:\mathrm{my}\:\mathrm{formulary},\:\mathrm{cannot}\:\mathrm{show}\:\mathrm{how}\right. \\ $$
Commented by ZiYangLee last updated on 25/Nov/20

$$\mathrm{oh}\:\mathrm{ok}\:\mathrm{thanks}\:\mathrm{sir}\:\mathrm{haha} \\ $$
