Question Number 169304 by mathlove last updated on 28/Apr/22
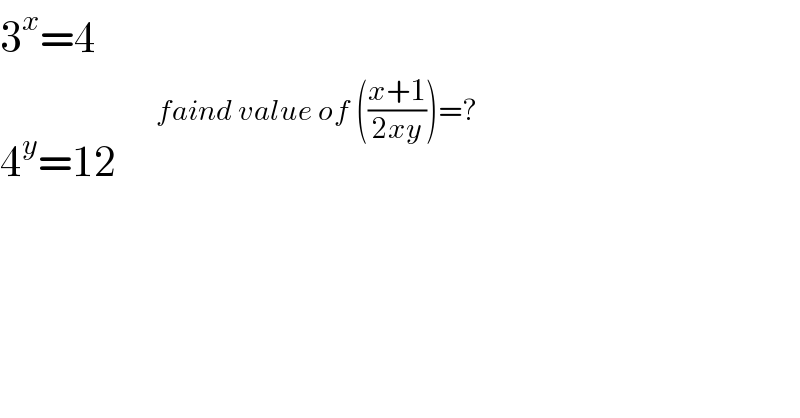
$$\mathrm{3}^{{x}} =\mathrm{4} \\ $$$$\mathrm{4}^{{y}} =\mathrm{12}\:\:\:\:\:\overset{{faind}\:{value}\:{of}\:\left(\frac{{x}+\mathrm{1}}{\mathrm{2}{xy}}\right)=?} {\:} \\ $$
Commented by infinityaction last updated on 28/Apr/22
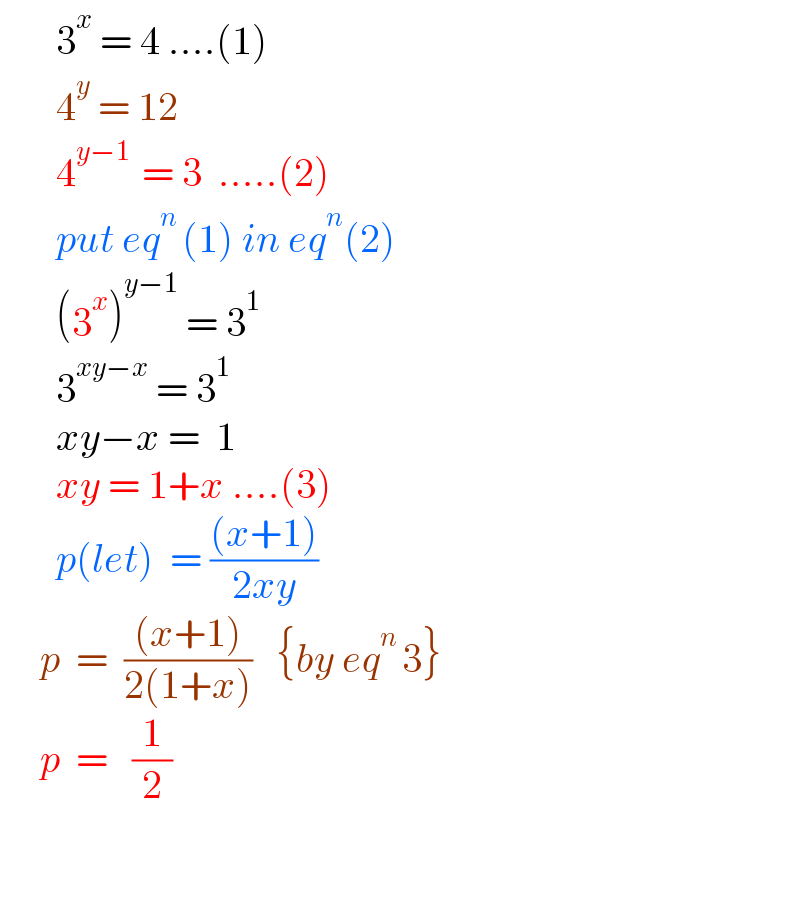
$$\:\:\:\:\:\:\:\mathrm{3}^{{x}} \:=\:\mathrm{4}\:….\left(\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{4}^{{y}} \:=\:\mathrm{12} \\ $$$$\:\:\:\:\:\:\:\mathrm{4}^{{y}−\mathrm{1}\:} \:=\:\mathrm{3}\:\:…..\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:{put}\:{eq}^{{n}\:} \left(\mathrm{1}\right)\:{in}\:{eq}^{{n}} \left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\left(\mathrm{3}^{{x}} \right)^{{y}−\mathrm{1}} \:=\:\mathrm{3}^{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\mathrm{3}^{{xy}−{x}} \:=\:\mathrm{3}^{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:{xy}−{x}\:=\:\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\:{xy}\:=\:\mathrm{1}+{x}\:….\left(\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:{p}\left({let}\right)\:\:=\:\frac{\left({x}+\mathrm{1}\right)}{\mathrm{2}{xy}} \\ $$$$\:\:\:\:\:{p}\:\:=\:\:\frac{\left({x}+\mathrm{1}\right)}{\mathrm{2}\left(\mathrm{1}+{x}\right)}\:\:\:\left\{{by}\:{eq}^{{n}\:} \mathrm{3}\right\}\: \\ $$$$\:\:\:\:\:{p}\:\:=\:\:\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$
Commented by mathlove last updated on 28/Apr/22

$${thanks} \\ $$
Commented by Mastermind last updated on 28/Apr/22
$${Wow},\:{you}\:{did}\:{a}\:{great}\:{job} \\ $$$${check}\:{my}\:{solution}\:{too} \\ $$
Commented by infinityaction last updated on 28/Apr/22

$${your}\:{solution}\:{is}\:{right}\: \\ $$
Answered by Mastermind last updated on 28/Apr/22
![Add log_3 and log_4 to both sides of the equations above respectively we have, log_3 3^x =log_3 4 and log_4 4^y =log_4 12 then, x=log_3 4 and y=log_4 12⇒ 1+log_4 3 Now, substitute it in (((x+1)/(2xy))) (((log_3 4+1)/(2[(log_3 4)(1+log_4 3)]))) (((log_3 4+1)/(2[(log_3 4+1)])))=(1/2) Mastermind](https://www.tinkutara.com/question/Q169307.png)
$$ \\ $$$${Add}\:{log}_{\mathrm{3}} \:{and}\:{log}_{\mathrm{4}} \:{to}\:{both}\:{sides}\:{of}\:{the} \\ $$$${equations}\:{above}\:{respectively} \\ $$$${we}\:{have}, \\ $$$${log}_{\mathrm{3}} \mathrm{3}^{{x}} ={log}_{\mathrm{3}} \mathrm{4}\:\:\:{and}\:{log}_{\mathrm{4}} \mathrm{4}^{{y}} ={log}_{\mathrm{4}} \mathrm{12} \\ $$$${then}, \\ $$$${x}={log}_{\mathrm{3}} \mathrm{4}\:{and}\:{y}={log}_{\mathrm{4}} \mathrm{12}\Rightarrow\:\mathrm{1}+{log}_{\mathrm{4}} \mathrm{3} \\ $$$${Now},\:{substitute}\:{it}\:{in}\:\left(\frac{{x}+\mathrm{1}}{\mathrm{2}{xy}}\right) \\ $$$$\left(\frac{{log}_{\mathrm{3}} \mathrm{4}+\mathrm{1}}{\mathrm{2}\left[\left({log}_{\mathrm{3}} \mathrm{4}\right)\left(\mathrm{1}+{log}_{\mathrm{4}} \mathrm{3}\right)\right]}\right) \\ $$$$\left(\frac{{log}_{\mathrm{3}} \mathrm{4}+\mathrm{1}}{\mathrm{2}\left[\left({log}_{\mathrm{3}} \mathrm{4}+\mathrm{1}\right)\right]}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$${Mastermind} \\ $$
