Question Number 169280 by mathlove last updated on 28/Apr/22
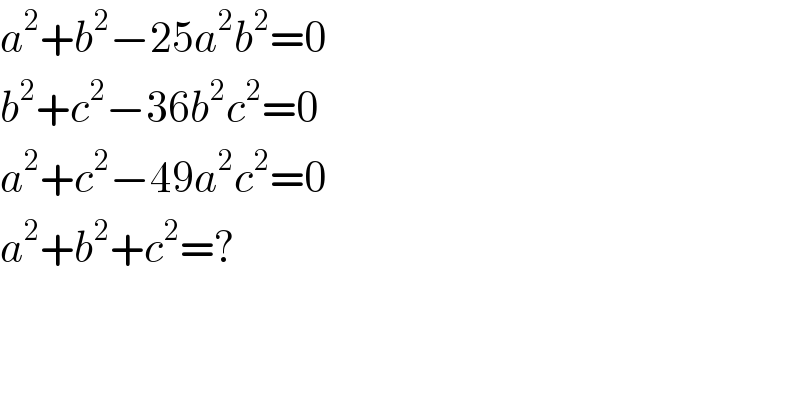
$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{25}{a}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{0} \\ $$$${b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{36}{b}^{\mathrm{2}} {c}^{\mathrm{2}} =\mathrm{0} \\ $$$${a}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{49}{a}^{\mathrm{2}} {c}^{\mathrm{2}} =\mathrm{0} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =? \\ $$
Answered by som(math1967) last updated on 28/Apr/22
![a^2 +b^2 =25a^2 b^2 (1/a^2 ) +(1/b^2 )=25.....i) same way (1/b^2 ) +(1/c^2 )=36 ....ii) (1/c^2 ) +(1/a^2 )=49.....iii) i)+ii)+iii) ∴ 2((1/a^2 ) +(1/b^2 ) +(1/c^2 ))= 110 ⇒(1/a^2 ) +(1/b^2 ) +(1/c^2 )=55 ....iv) iv) −ii) (1/a^2 )= 55−36=19 ⇒a^2 =(1/(19)) (1/b^2 )=25−19=6⇒b^2 =(1/6) (1/c^2 )=49−19=30⇒c^2 =(1/(30)) a^2 +b^2 +c^2 =(1/(19))+(1/6)+(1/(30))=(1/(19))+(1/5)=((24)/(95)) [ if a,b,c ≠0] if a,b,c=0, then a^2 +b^2 +c^2 =0](https://www.tinkutara.com/question/Q169283.png)
$$\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{25}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\left.\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }=\mathrm{25}…..{i}\right) \\ $$$${same}\:{way} \\ $$$$\left.\:\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }=\mathrm{36}\:\:….{ii}\right) \\ $$$$\left.\:\frac{\mathrm{1}}{{c}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{a}^{\mathrm{2}} }=\mathrm{49}…..{iii}\right) \\ $$$$\left.{i}\left.\right)\left.+{ii}\right)+{iii}\right) \\ $$$$\therefore\:\mathrm{2}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }\right)=\:\mathrm{110} \\ $$$$\left.\:\Rightarrow\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }=\mathrm{55}\:….{iv}\right) \\ $$$$\left.{i}\left.{v}\right)\:−{ii}\right) \\ $$$$\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} }=\:\mathrm{55}−\mathrm{36}=\mathrm{19} \\ $$$$\Rightarrow{a}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{19}} \\ $$$$\frac{\mathrm{1}}{{b}^{\mathrm{2}} }=\mathrm{25}−\mathrm{19}=\mathrm{6}\Rightarrow{b}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\:\frac{\mathrm{1}}{{c}^{\mathrm{2}} }=\mathrm{49}−\mathrm{19}=\mathrm{30}\Rightarrow{c}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{30}} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{19}}+\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{30}}=\frac{\mathrm{1}}{\mathrm{19}}+\frac{\mathrm{1}}{\mathrm{5}}=\frac{\mathrm{24}}{\mathrm{95}} \\ $$$$\left[\:\boldsymbol{{if}}\:\boldsymbol{{a}},\boldsymbol{{b}},\boldsymbol{{c}}\:\neq\mathrm{0}\right] \\ $$$$\boldsymbol{{if}}\:\boldsymbol{{a}},\boldsymbol{{b}},\boldsymbol{{c}}=\mathrm{0},\:\boldsymbol{{then}}\:\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{{c}}^{\mathrm{2}} =\mathrm{0} \\ $$
Commented by mathlove last updated on 28/Apr/22

$${thanks} \\ $$
Commented by SLVR last updated on 05/May/22
$${great}\:{sir}…{quite}?{good} \\ $$
