Question Number 175410 by Stephan last updated on 29/Aug/22
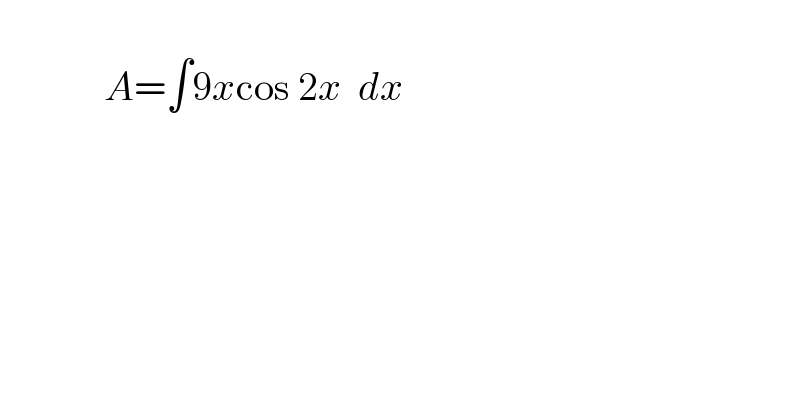
$$\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{A}=\int\mathrm{9}{x}\mathrm{cos}\:\mathrm{2}{x}\:\:{dx} \\ $$$$ \\ $$
Answered by MikeH last updated on 29/Aug/22
![let { ((u = x⇒ du = dx)),((dv = cos 2x dx ⇒ v = (1/2) sin 2x)) :} A = 9[((x sin 2x)/2)−(1/2)∫sin 2x dx] A = (9/2)(x sin 2x +(1/2) cos 2x)+k](https://www.tinkutara.com/question/Q175413.png)
$$\mathrm{let}\:\begin{cases}{{u}\:=\:{x}\Rightarrow\:{du}\:=\:{dx}}\\{{dv}\:=\:\mathrm{cos}\:\mathrm{2}{x}\:{dx}\:\Rightarrow\:{v}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{sin}\:\mathrm{2}{x}}\end{cases} \\ $$$${A}\:=\:\mathrm{9}\left[\frac{{x}\:\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{sin}\:\mathrm{2}{x}\:{dx}\right]\: \\ $$$${A}\:=\:\frac{\mathrm{9}}{\mathrm{2}}\left({x}\:\mathrm{sin}\:\mathrm{2}{x}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{cos}\:\mathrm{2}{x}\right)+{k} \\ $$
