Question Number 20842 by Tinkutara last updated on 04/Sep/17

$$\mathrm{Acceleration}\:\mathrm{of}\:\mathrm{a}\:\mathrm{particle}\:\mathrm{which}\:\mathrm{is}\:\mathrm{at} \\ $$$$\mathrm{rest}\:\mathrm{at}\:{x}\:=\:\mathrm{0}\:\mathrm{is}\:\overset{\rightarrow} {{a}}\:=\:\left(\mathrm{4}\:−\:\mathrm{2}{x}\right)\:\overset{\wedge} {{i}}.\:\mathrm{Select} \\ $$$$\mathrm{the}\:\mathrm{correct}\:\mathrm{alternative}\left(\mathrm{s}\right). \\ $$$$\left({a}\right)\:\mathrm{Maximum}\:\mathrm{speed}\:\mathrm{of}\:\mathrm{the}\:\mathrm{particle}\:\mathrm{is} \\ $$$$\mathrm{4}\:\mathrm{units} \\ $$$$\left({b}\right)\:\mathrm{Particle}\:\mathrm{further}\:\mathrm{comes}\:\mathrm{to}\:\mathrm{rest}\:\mathrm{at} \\ $$$${x}\:=\:\mathrm{4} \\ $$$$\left({c}\right)\:\mathrm{Particle}\:\mathrm{oscillates}\:\mathrm{about}\:{x}\:=\:\mathrm{2} \\ $$$$\left({d}\right)\:\mathrm{Particle}\:\mathrm{will}\:\mathrm{continuously}\:\mathrm{accelerate} \\ $$$$\mathrm{along}\:\mathrm{the}\:{x}-\mathrm{axis}. \\ $$
Answered by ajfour last updated on 09/Sep/17
![((v_x dv_x )/dx)=4−2x ⇒ ∫_0 ^( v_x ) v_x dv_x =∫_0 ^( x) (4−2x)dx ⇒ (v_x ^2 /2)=4x−x^2 ⇒ v_x ^2 =2[4−(x−2)^2 ] ⇒ particle comes to rest at x=4. maximum speed at x=2 and is (v_x )_(max) =2(√2) units. ⇒ ∫_0 ^( x) (dx/( (√(2^2 −(x−2)^2 )))) = ±(√2)∫_0 ^( t) dt ⇒sin^(−1) (((x−2)/2))−sin^(−1) (−1)=±(√2)t ⇒ sin^(−1) (((x−2)/2))=±(√2)t−π/2 x=2+2sin (±(√2)t−π/2) or x=2−cos ((√2)t) is the equation of motion. ⇒ particle oscillates about x=2. (b) and (c) are the correct options.](https://www.tinkutara.com/question/Q20844.png)
$$\frac{{v}_{{x}} {dv}_{{x}} }{{dx}}=\mathrm{4}−\mathrm{2}{x} \\ $$$$\Rightarrow\:\int_{\mathrm{0}} ^{\:\:{v}_{{x}} } {v}_{{x}} {dv}_{{x}} =\int_{\mathrm{0}} ^{\:\:{x}} \left(\mathrm{4}−\mathrm{2}{x}\right){dx} \\ $$$$\Rightarrow\:\:\:\frac{{v}_{{x}} ^{\mathrm{2}} }{\mathrm{2}}=\mathrm{4}{x}−{x}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:{v}_{{x}} ^{\mathrm{2}} =\mathrm{2}\left[\mathrm{4}−\left({x}−\mathrm{2}\right)^{\mathrm{2}} \right] \\ $$$$\Rightarrow\:{particle}\:{comes}\:{to}\:{rest}\:{at}\:{x}=\mathrm{4}. \\ $$$${maximum}\:{speed}\:{at}\:{x}=\mathrm{2}\:{and}\:{is} \\ $$$$\left({v}_{{x}} \right)_{{max}} =\mathrm{2}\sqrt{\mathrm{2}}\:{units}. \\ $$$$\Rightarrow\:\:\int_{\mathrm{0}} ^{\:\:{x}} \:\frac{{dx}}{\:\sqrt{\mathrm{2}^{\mathrm{2}} −\left({x}−\mathrm{2}\right)^{\mathrm{2}} }}\:=\:\pm\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\:{t}} {dt} \\ $$$$\Rightarrow\mathrm{sin}^{−\mathrm{1}} \left(\frac{{x}−\mathrm{2}}{\mathrm{2}}\right)−\mathrm{sin}^{−\mathrm{1}} \left(−\mathrm{1}\right)=\pm\sqrt{\mathrm{2}}{t} \\ $$$$\Rightarrow\:\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{{x}−\mathrm{2}}{\mathrm{2}}\right)=\pm\sqrt{\mathrm{2}}{t}−\pi/\mathrm{2} \\ $$$${x}=\mathrm{2}+\mathrm{2sin}\:\left(\pm\sqrt{\mathrm{2}}{t}−\pi/\mathrm{2}\right) \\ $$$${or}\:\:\:\:{x}=\mathrm{2}−\mathrm{cos}\:\left(\sqrt{\mathrm{2}}{t}\right) \\ $$$$\:\:\:{is}\:{the}\:{equation}\:{of}\:{motion}. \\ $$$$\Rightarrow\:\:{particle}\:{oscillates}\:{about}\:{x}=\mathrm{2}. \\ $$$$\left(\boldsymbol{{b}}\right)\:{and}\:\left(\boldsymbol{{c}}\right)\:{are}\:{the}\:{correct}\:{options}. \\ $$
Commented by ajfour last updated on 09/Sep/17

$${thanks},\:{i}\:{shall}\:{be}\:{careful}. \\ $$
Commented by alex041103 last updated on 09/Sep/17
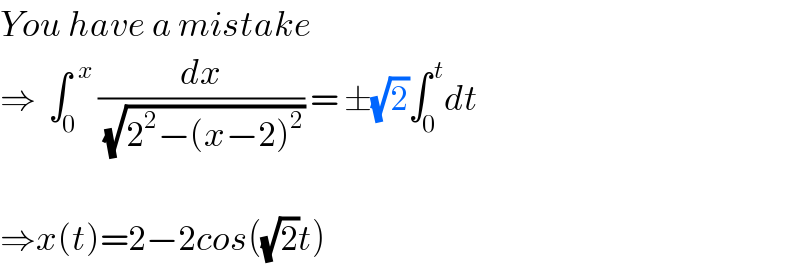
$${You}\:{have}\:{a}\:{mistake} \\ $$$$\Rightarrow\:\:\int_{\mathrm{0}} ^{\:\:{x}} \:\frac{{dx}}{\:\sqrt{\mathrm{2}^{\mathrm{2}} −\left({x}−\mathrm{2}\right)^{\mathrm{2}} }}\:=\:\pm\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\:{t}} {dt} \\ $$$$ \\ $$$$\Rightarrow{x}\left({t}\right)=\mathrm{2}−\mathrm{2}{cos}\left(\sqrt{\mathrm{2}}{t}\right) \\ $$
Commented by Tinkutara last updated on 04/Sep/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
