Question Number 129418 by mnjuly1970 last updated on 15/Jan/21
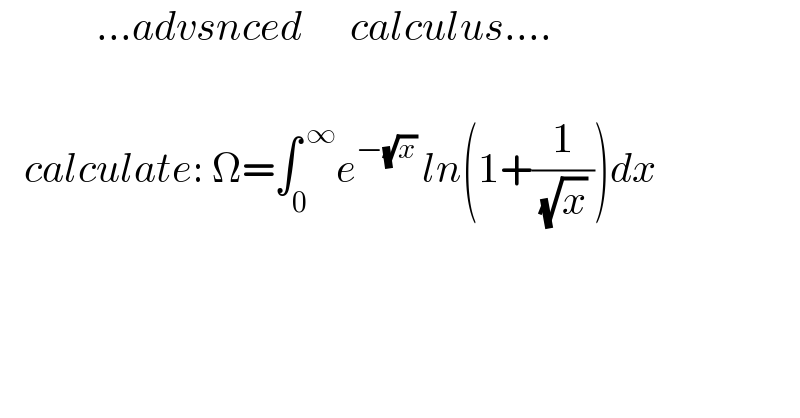
$$\:\:\:\:\:\:\:\:\:\:\:\:…{advsnced}\:\:\:\:\:\:{calculus}….\:\: \\ $$$$ \\ $$$$\:\:\:{calculate}:\:\Omega=\int_{\mathrm{0}} ^{\:\infty} {e}^{−\sqrt{{x}}\:} {ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{{x}}\:}\right){dx} \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 15/Jan/21

$$\int_{\mathrm{0}} ^{\infty} {e}^{−\sqrt{{x}}} {log}\left(\mathrm{1}+\sqrt{{x}}\right)−\int_{\mathrm{0}} ^{\infty} {e}^{−\sqrt{{x}}} {log}\left(\sqrt{{x}}\right){dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} {te}^{−{t}} {log}\left(\mathrm{1}+{t}\right)−\mathrm{2}\int_{\mathrm{0}} ^{\infty} {te}^{−{t}} {log}\left({t}\right) \\ $$$$=\mathrm{2}−\mathrm{2}\left(\Gamma'\left(\mathrm{2}\right)\right)=\mathrm{2}−\mathrm{2}\left(−\gamma+\mathrm{1}\right)=\mathrm{2}\gamma \\ $$
Commented by mnjuly1970 last updated on 15/Jan/21

$${excellent}…{grateful}.. \\ $$
Answered by mindispower last updated on 15/Jan/21
![(√x)=t ⇒∫_0 ^∞ e^(−t) ln(1+(1/t)).2tdt ∫ln(1+t)te^(−t) dt by part ∫te^(−t) dt=−(t+1)e^(−t) dt ∫_0 ^∞ ln(1+t)te^(−t) dt=[−(t+1)e^(−t) ln(1+t)]_0 ^∞ +∫(((t+1)e^(−t) )/(t+1))dt =∫_0 ^∞ e^(−t) dt=Γ(1)=1 ∫_0 ^∞ te^(−t) ln(t)dt=∂_x ∫_0 ^∞ t^(x−1) e^(−t) dt∣_(x=2) =Γ′(2)=Γ(2)Ψ(2) =Ψ(2)=1+Ψ(1)=1−γ ∫_0 ^∞ e^(−t) ln(1+(1/t)).2tdt=2∫_0 ^∞ e^(−t) ln(1+t)tdt−2∫_0 ^∞ e^(−t) tln(t)dt =2.1−2(1−γ)=2γ](https://www.tinkutara.com/question/Q129432.png)
$$\sqrt{{x}}={t} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{t}}\right).\mathrm{2}{tdt} \\ $$$$\int{ln}\left(\mathrm{1}+{t}\right){te}^{−{t}} {dt}\:\:{by}\:{part} \\ $$$$\int{te}^{−{t}} {dt}=−\left({t}+\mathrm{1}\right){e}^{−{t}} {dt} \\ $$$$\int_{\mathrm{0}} ^{\infty} {ln}\left(\mathrm{1}+{t}\right){te}^{−{t}} {dt}=\left[−\left({t}+\mathrm{1}\right){e}^{−{t}} {ln}\left(\mathrm{1}+{t}\right)\right]_{\mathrm{0}} ^{\infty} +\int\frac{\left({t}+\mathrm{1}\right){e}^{−{t}} }{{t}+\mathrm{1}}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {dt}=\Gamma\left(\mathrm{1}\right)=\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\infty} {te}^{−{t}} {ln}\left({t}\right){dt}=\partial_{{x}} \int_{\mathrm{0}} ^{\infty} {t}^{{x}−\mathrm{1}} {e}^{−{t}} {dt}\mid_{{x}=\mathrm{2}} =\Gamma'\left(\mathrm{2}\right)=\Gamma\left(\mathrm{2}\right)\Psi\left(\mathrm{2}\right) \\ $$$$=\Psi\left(\mathrm{2}\right)=\mathrm{1}+\Psi\left(\mathrm{1}\right)=\mathrm{1}−\gamma \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{t}}\right).\mathrm{2}{tdt}=\mathrm{2}\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {ln}\left(\mathrm{1}+{t}\right){tdt}−\mathrm{2}\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {tln}\left({t}\right){dt} \\ $$$$=\mathrm{2}.\mathrm{1}−\mathrm{2}\left(\mathrm{1}−\gamma\right)=\mathrm{2}\gamma \\ $$
Commented by mnjuly1970 last updated on 16/Jan/21
$${very}\:{nice}\:{as}\:{always}… \\ $$
Answered by Lordose last updated on 16/Jan/21
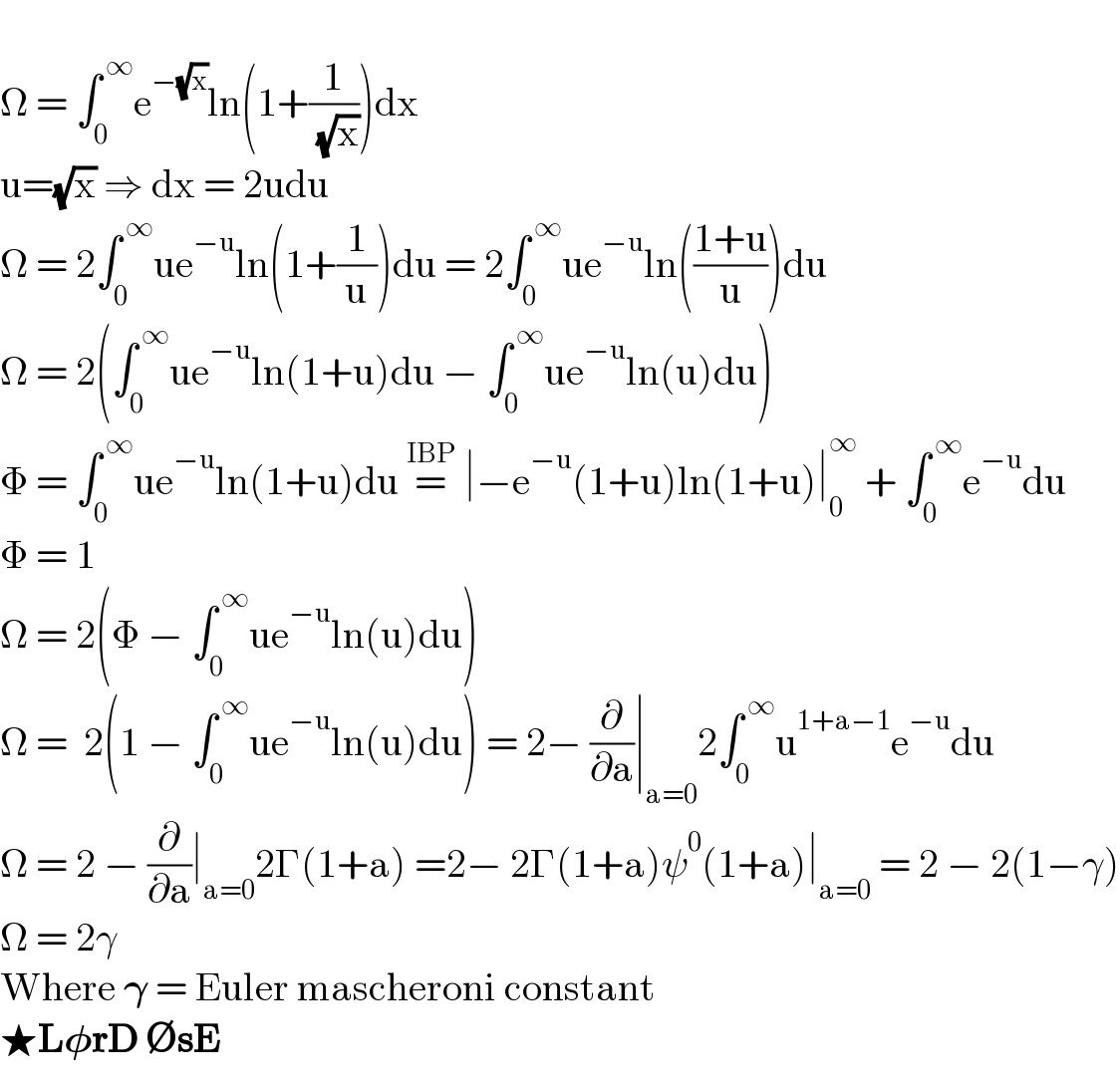
$$ \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\infty} \mathrm{e}^{−\sqrt{\mathrm{x}}} \mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}}}\right)\mathrm{dx} \\ $$$$\mathrm{u}=\sqrt{\mathrm{x}}\:\Rightarrow\:\mathrm{dx}\:=\:\mathrm{2udu} \\ $$$$\Omega\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \mathrm{ue}^{−\mathrm{u}} \mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{u}}\right)\mathrm{du}\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \mathrm{ue}^{−\mathrm{u}} \mathrm{ln}\left(\frac{\mathrm{1}+\mathrm{u}}{\mathrm{u}}\right)\mathrm{du} \\ $$$$\Omega\:=\:\mathrm{2}\left(\int_{\mathrm{0}} ^{\:\infty} \mathrm{ue}^{−\mathrm{u}} \mathrm{ln}\left(\mathrm{1}+\mathrm{u}\right)\mathrm{du}\:−\:\int_{\mathrm{0}} ^{\:\infty} \mathrm{ue}^{−\mathrm{u}} \mathrm{ln}\left(\mathrm{u}\right)\mathrm{du}\right) \\ $$$$\Phi\:=\:\int_{\mathrm{0}} ^{\:\infty} \mathrm{ue}^{−\mathrm{u}} \mathrm{ln}\left(\mathrm{1}+\mathrm{u}\right)\mathrm{du}\:\overset{\mathrm{IBP}} {=}\:\mid−\mathrm{e}^{−\mathrm{u}} \left(\mathrm{1}+\mathrm{u}\right)\mathrm{ln}\left(\mathrm{1}+\mathrm{u}\right)\mid_{\mathrm{0}} ^{\infty} \:+\:\int_{\mathrm{0}} ^{\:\infty} \mathrm{e}^{−\mathrm{u}} \mathrm{du} \\ $$$$\Phi\:=\:\mathrm{1} \\ $$$$\Omega\:=\:\mathrm{2}\left(\Phi\:−\:\int_{\mathrm{0}} ^{\:\infty} \mathrm{ue}^{−\mathrm{u}} \mathrm{ln}\left(\mathrm{u}\right)\mathrm{du}\right) \\ $$$$\Omega\:=\:\:\mathrm{2}\left(\mathrm{1}\:−\:\int_{\mathrm{0}} ^{\:\infty} \mathrm{ue}^{−\mathrm{u}} \mathrm{ln}\left(\mathrm{u}\right)\mathrm{du}\right)\:=\:\mathrm{2}−\:\frac{\partial}{\partial\mathrm{a}}\mid_{\mathrm{a}=\mathrm{0}} \mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \mathrm{u}^{\mathrm{1}+\mathrm{a}−\mathrm{1}} \mathrm{e}^{−\mathrm{u}} \mathrm{du} \\ $$$$\Omega\:=\:\mathrm{2}\:−\:\frac{\partial}{\partial\mathrm{a}}\mid_{\mathrm{a}=\mathrm{0}} \mathrm{2}\Gamma\left(\mathrm{1}+\mathrm{a}\right)\:=\mathrm{2}−\:\mathrm{2}\Gamma\left(\mathrm{1}+\mathrm{a}\right)\psi^{\mathrm{0}} \left(\mathrm{1}+\mathrm{a}\right)\mid_{\mathrm{a}=\mathrm{0}} \:=\:\mathrm{2}\:−\:\mathrm{2}\left(\mathrm{1}−\gamma\right) \\ $$$$\Omega\:=\:\mathrm{2}\gamma \\ $$$$\mathrm{Where}\:\boldsymbol{\gamma}\:=\:\mathrm{Euler}\:\mathrm{mascheroni}\:\mathrm{constant} \\ $$$$\bigstar\boldsymbol{\mathrm{L}\phi\mathrm{rD}}\:\boldsymbol{\varnothing\mathrm{sE}} \\ $$
Commented by mnjuly1970 last updated on 16/Jan/21

$${thank}\:{you}\:{mr}\:{lordos}… \\ $$
