Question Number 95653 by rb222 last updated on 26/May/20
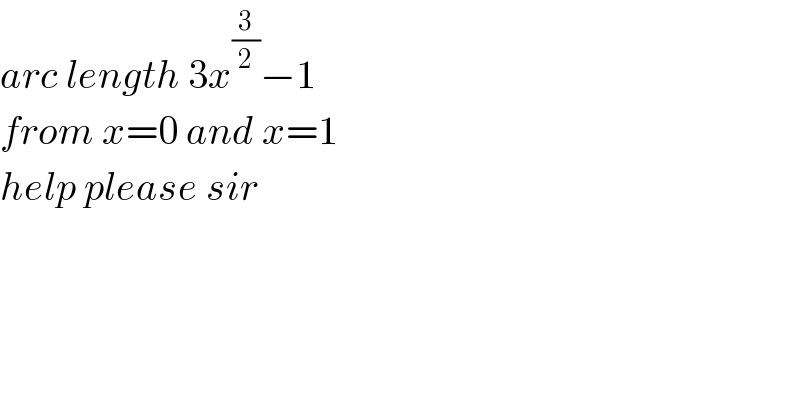
$${arc}\:{length}\:\mathrm{3}{x}^{\frac{\mathrm{3}}{\mathrm{2}}} −\mathrm{1}\: \\ $$$${from}\:{x}=\mathrm{0}\:{and}\:{x}=\mathrm{1}\: \\ $$$${help}\:{please}\:{sir} \\ $$
Answered by john santu last updated on 26/May/20
![Arc L = ∫_(0 ) ^1 (√(1+((dy/dx))^2 )) dx (dy/dx) = (9/2)(√x) ∫_0 ^1 (√(1+((81x)/4))) dx = (1/2)∫_0 ^1 (√(4+81x)) dx =(1/2) [(((4+81x)^(3/2) )/((243)/2)) ]_0 ^1 =((85(√(85 )) −8 )/(243))](https://www.tinkutara.com/question/Q95659.png)
$$\mathrm{Arc}\:\mathrm{L}\:=\:\underset{\mathrm{0}\:} {\overset{\mathrm{1}} {\int}}\sqrt{\mathrm{1}+\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)^{\mathrm{2}} }\:\mathrm{dx}\: \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{9}}{\mathrm{2}}\sqrt{\mathrm{x}}\: \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\sqrt{\mathrm{1}+\frac{\mathrm{81x}}{\mathrm{4}}}\:\mathrm{dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\sqrt{\mathrm{4}+\mathrm{81x}}\:\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\left[\frac{\left(\mathrm{4}+\mathrm{81x}\right)^{\mathrm{3}/\mathrm{2}} }{\frac{\mathrm{243}}{\mathrm{2}}}\:\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{85}\sqrt{\mathrm{85}\:}\:−\mathrm{8}\:}{\mathrm{243}}\: \\ $$
Answered by MAB last updated on 26/May/20
![dl=(√((dx)^2 +(dy)^2 )) dl=(√(1+((dy/dx))^2 ))dx l=∫_0 ^1 (√(1+(f ′(x))^2 ))dx l=∫_0 ^1 (√(1+((81)/4)x))dx l=[(8/(243))(1+((81)/4)x)^(3/2) ]_0 ^1 l=((85(√(85))−8)/(243))](https://www.tinkutara.com/question/Q95661.png)
$${dl}=\sqrt{\left({dx}\right)^{\mathrm{2}} +\left({dy}\right)^{\mathrm{2}} } \\ $$$${dl}=\sqrt{\mathrm{1}+\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} }{dx} \\ $$$${l}=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}+\left({f}\:'\left({x}\right)\right)^{\mathrm{2}} }{dx} \\ $$$${l}=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}+\frac{\mathrm{81}}{\mathrm{4}}{x}}{dx} \\ $$$${l}=\left[\frac{\mathrm{8}}{\mathrm{243}}\left(\mathrm{1}+\frac{\mathrm{81}}{\mathrm{4}}{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$${l}=\frac{\mathrm{85}\sqrt{\mathrm{85}}−\mathrm{8}}{\mathrm{243}} \\ $$
Commented by rb222 last updated on 27/May/20

$${thanks}\:{sir} \\ $$
Commented by MAB last updated on 06/Jun/20

$${you}\:{are}\:{welcome} \\ $$
