Question Number 62747 by Mikael last updated on 24/Jun/19
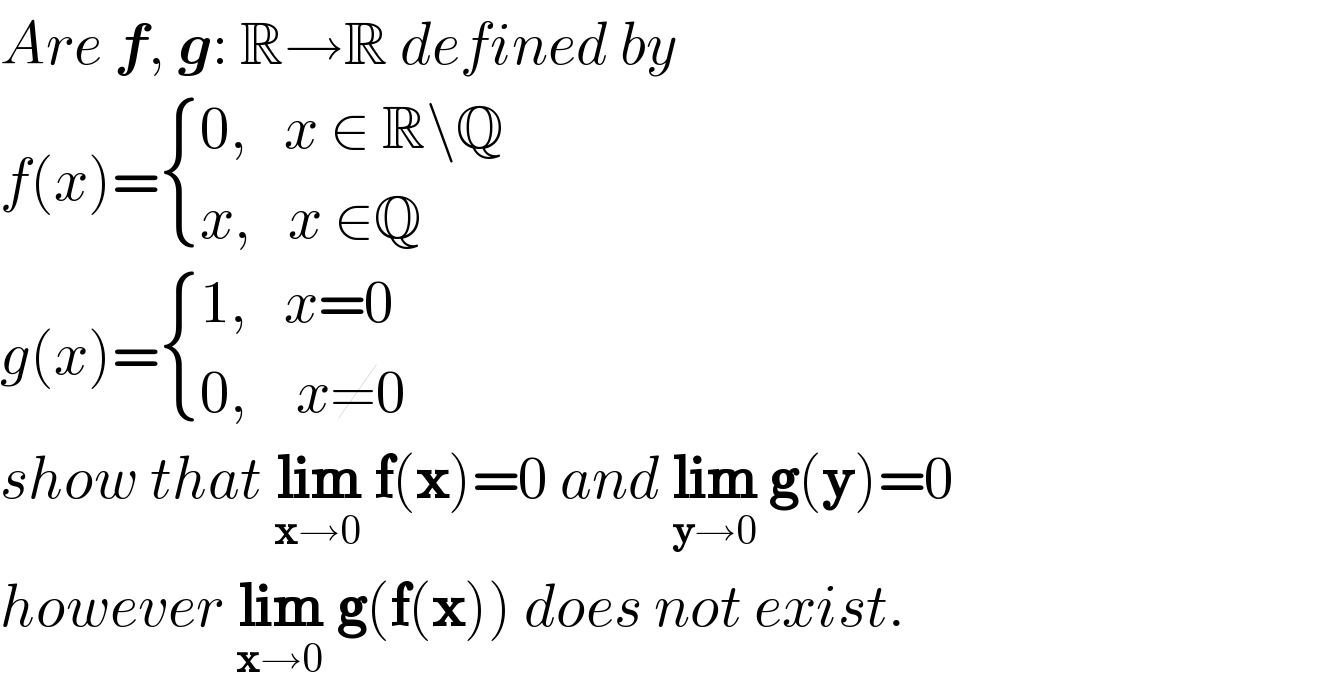
$${Are}\:\boldsymbol{{f}},\:\boldsymbol{{g}}:\:\mathbb{R}\rightarrow\mathbb{R}\:{defined}\:{by} \\ $$$${f}\left({x}\right)=\begin{cases}{\mathrm{0},\:\:\:{x}\:\in\:\mathbb{R}\backslash\mathbb{Q}}\\{{x},\:\:\:{x}\:\in\mathbb{Q}}\end{cases} \\ $$$${g}\left({x}\right)=\begin{cases}{\mathrm{1},\:\:\:{x}=\mathrm{0}}\\{\mathrm{0},\:\:\:\:{x}\neq\mathrm{0}}\end{cases} \\ $$$${show}\:{that}\:\underset{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{0}} {\boldsymbol{\mathrm{lim}}}\:\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)=\mathrm{0}\:{and}\:\underset{\boldsymbol{\mathrm{y}}\rightarrow\mathrm{0}} {\boldsymbol{\mathrm{lim}}}\:\boldsymbol{\mathrm{g}}\left(\boldsymbol{\mathrm{y}}\right)=\mathrm{0} \\ $$$${however}\:\underset{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{0}} {\boldsymbol{\mathrm{lim}}}\:\boldsymbol{\mathrm{g}}\left(\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)\right)\:{does}\:{not}\:{exist}. \\ $$
Answered by MJS last updated on 25/Jun/19
![x∈R\Q: lim_(x→0) f(x)=0 is trivial because f(x)=0 in this case x∈Q: lim_(x→0) f(x)=lim_(p→0) (p/q) ∀p∈Z∧∀q∈N^★ ⇒ ⇒ lim_(x→0) f(x)=lim_(p→0) (p/q)=0 lim_(x→0) g(x)=0 because g(x)=0 for x∈[−ε; ε]∀ε∈R^+ lim_(x→0) g(f(x)) does not exist because ∀x∈R\Q g(f(x))=1 but ∀x∈Q g(f(x))=0 ⇒ ⇒ lim_(x∈R\Q→0) g(f(x))=1 ∧ lim_(x∈Q→0) g(f(x))=0 ⇒ limit ∀x∈R doesn′t exist](https://www.tinkutara.com/question/Q62783.png)
$${x}\in\mathbb{R}\backslash\mathbb{Q}:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{f}\left({x}\right)=\mathrm{0}\:\mathrm{is}\:\mathrm{trivial}\:\mathrm{because}\:{f}\left({x}\right)=\mathrm{0}\:\mathrm{in}\:\mathrm{this}\:\mathrm{case} \\ $$$${x}\in\mathbb{Q}:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{f}\left({x}\right)=\underset{{p}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{p}}{{q}}\:\forall{p}\in\mathbb{Z}\wedge\forall{q}\in\mathbb{N}^{\bigstar} \:\Rightarrow \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{f}\left({x}\right)=\underset{{p}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{p}}{{q}}=\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{g}\left({x}\right)=\mathrm{0}\:\mathrm{because}\:{g}\left({x}\right)=\mathrm{0}\:\mathrm{for}\:{x}\in\left[−\epsilon;\:\epsilon\right]\forall\epsilon\in\mathbb{R}^{+} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{g}\left({f}\left({x}\right)\right)\:\mathrm{does}\:\mathrm{not}\:\mathrm{exist}\:\mathrm{because}\:\forall{x}\in\mathbb{R}\backslash\mathbb{Q} \\ $$$${g}\left({f}\left({x}\right)\right)=\mathrm{1}\:\mathrm{but}\:\forall{x}\in\mathbb{Q}\:{g}\left({f}\left({x}\right)\right)=\mathrm{0}\:\Rightarrow\: \\ $$$$\Rightarrow\:\underset{{x}\in\mathbb{R}\backslash\mathbb{Q}\rightarrow\mathrm{0}} {\mathrm{lim}}{g}\left({f}\left({x}\right)\right)=\mathrm{1}\:\wedge\:\underset{{x}\in\mathbb{Q}\rightarrow\mathrm{0}} {\mathrm{lim}}{g}\left({f}\left({x}\right)\right)=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{limit}\:\forall{x}\in\mathbb{R}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist} \\ $$
Commented by Mikael last updated on 25/Jun/19

$${thank}\:{you}\:{Sir}. \\ $$
