Question Number 113634 by eric last updated on 14/Sep/20

$${Bonjour}\:{besoin}\:{d}'{aide} \\ $$$${Calculer}\:\int{ln}\left({cosx}\right){dx} \\ $$
Answered by Olaf last updated on 14/Sep/20
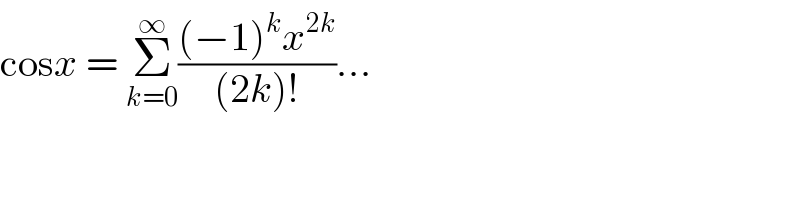
$$\mathrm{cos}{x}\:=\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} {x}^{\mathrm{2}{k}} }{\left(\mathrm{2}{k}\right)!}… \\ $$$$ \\ $$
Answered by MJS_new last updated on 18/Sep/20
![∫ln cos x dx= [by parts] =xln cos x +∫xtan x dx ∫xtan x dx=−i∫x((e^(ix) −e^(−ix) )/(e^(ix) +e^(ix) ))dx= =−i∫x((e^(2ix) −1)/(e^(2ix) +1))dx= [t=e^(2ix) ⇔ x=−(i/2)ln t → dx=−(i/(2t))dt] =(i/4)∫ln t ((t−1)/(t(t+1)))dt= (i/2)∫((ln t)/(t+1))dt−(i/4)∫((ln t)/t)dt (i/2)∫((ln t)/(t+1))dt= [by parts] =(i/2)ln t ln (t+1) −(i/2)∫((ln (t+1))/t)dt= =(i/2)ln t ln (t+1) +(i/2)Li_2 (−t) −(i/4)∫((ln t)/t)dt= [by parts] =(i/8)(ln t)^2 ⇒ ∫xtan x dx=(i/2)ln t ln (t+1) +(i/2)Li_2 (−t) +(i/8)(ln t)^2 = =(i/2)ln e^(2ix) ln (e^(2ix) +1) +(i/2)Li_2 (−e^(2ix) ) +(i/8)(ln e^(2ix) )^2 = =−(i/2)x^2 −xln (e^(2ix) +1) +(i/2)Li_2 (−e^(2ix) ) ⇒ ∫ln cos x dx= =xln cos x −(i/2)x^2 −xln (e^(2ix) +1) +(i/2)Li_2 (−e^(2ix) ) +C hopefully I made no errors, please check!](https://www.tinkutara.com/question/Q113699.png)
$$\int\mathrm{ln}\:\mathrm{cos}\:{x}\:{dx}= \\ $$$$\:\:\:\:\:\left[\mathrm{by}\:\mathrm{parts}\right] \\ $$$$={x}\mathrm{ln}\:\mathrm{cos}\:{x}\:+\int{x}\mathrm{tan}\:{x}\:{dx} \\ $$$$ \\ $$$$\int{x}\mathrm{tan}\:{x}\:{dx}=−\mathrm{i}\int{x}\frac{\mathrm{e}^{\mathrm{i}{x}} −\mathrm{e}^{−\mathrm{i}{x}} }{\mathrm{e}^{\mathrm{i}{x}} +\mathrm{e}^{\mathrm{i}{x}} }{dx}= \\ $$$$=−\mathrm{i}\int{x}\frac{\mathrm{e}^{\mathrm{2i}{x}} −\mathrm{1}}{\mathrm{e}^{\mathrm{2i}{x}} +\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{e}^{\mathrm{2i}{x}} \:\Leftrightarrow\:{x}=−\frac{\mathrm{i}}{\mathrm{2}}\mathrm{ln}\:{t}\:\rightarrow\:{dx}=−\frac{\mathrm{i}}{\mathrm{2}{t}}{dt}\right] \\ $$$$=\frac{\mathrm{i}}{\mathrm{4}}\int\mathrm{ln}\:{t}\:\frac{{t}−\mathrm{1}}{{t}\left({t}+\mathrm{1}\right)}{dt}= \\ $$$$\frac{\mathrm{i}}{\mathrm{2}}\int\frac{\mathrm{ln}\:{t}}{{t}+\mathrm{1}}{dt}−\frac{\mathrm{i}}{\mathrm{4}}\int\frac{\mathrm{ln}\:{t}}{{t}}{dt} \\ $$$$ \\ $$$$\frac{\mathrm{i}}{\mathrm{2}}\int\frac{\mathrm{ln}\:{t}}{{t}+\mathrm{1}}{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{by}\:\mathrm{parts}\right] \\ $$$$=\frac{\mathrm{i}}{\mathrm{2}}\mathrm{ln}\:{t}\:\mathrm{ln}\:\left({t}+\mathrm{1}\right)\:−\frac{\mathrm{i}}{\mathrm{2}}\int\frac{\mathrm{ln}\:\left({t}+\mathrm{1}\right)}{{t}}{dt}= \\ $$$$=\frac{\mathrm{i}}{\mathrm{2}}\mathrm{ln}\:{t}\:\mathrm{ln}\:\left({t}+\mathrm{1}\right)\:+\frac{\mathrm{i}}{\mathrm{2}}\mathrm{Li}_{\mathrm{2}} \:\left(−{t}\right) \\ $$$$ \\ $$$$−\frac{\mathrm{i}}{\mathrm{4}}\int\frac{\mathrm{ln}\:{t}}{{t}}{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{by}\:\mathrm{parts}\right] \\ $$$$=\frac{\mathrm{i}}{\mathrm{8}}\left(\mathrm{ln}\:{t}\right)^{\mathrm{2}} \\ $$$$ \\ $$$$\Rightarrow \\ $$$$\int{x}\mathrm{tan}\:{x}\:{dx}=\frac{\mathrm{i}}{\mathrm{2}}\mathrm{ln}\:{t}\:\mathrm{ln}\:\left({t}+\mathrm{1}\right)\:+\frac{\mathrm{i}}{\mathrm{2}}\mathrm{Li}_{\mathrm{2}} \:\left(−{t}\right)\:+\frac{\mathrm{i}}{\mathrm{8}}\left(\mathrm{ln}\:{t}\right)^{\mathrm{2}} = \\ $$$$=\frac{\mathrm{i}}{\mathrm{2}}\mathrm{ln}\:\mathrm{e}^{\mathrm{2i}{x}} \:\mathrm{ln}\:\left(\mathrm{e}^{\mathrm{2i}{x}} +\mathrm{1}\right)\:+\frac{\mathrm{i}}{\mathrm{2}}\mathrm{Li}_{\mathrm{2}} \:\left(−\mathrm{e}^{\mathrm{2i}{x}} \right)\:+\frac{\mathrm{i}}{\mathrm{8}}\left(\mathrm{ln}\:\mathrm{e}^{\mathrm{2i}{x}} \right)^{\mathrm{2}} = \\ $$$$=−\frac{\mathrm{i}}{\mathrm{2}}{x}^{\mathrm{2}} −{x}\mathrm{ln}\:\left(\mathrm{e}^{\mathrm{2i}{x}} +\mathrm{1}\right)\:+\frac{\mathrm{i}}{\mathrm{2}}\mathrm{L}{i}_{\mathrm{2}} \:\left(−\mathrm{e}^{\mathrm{2i}{x}} \right) \\ $$$$\Rightarrow \\ $$$$\int\mathrm{ln}\:\mathrm{cos}\:{x}\:{dx}= \\ $$$$={x}\mathrm{ln}\:\mathrm{cos}\:{x}\:−\frac{\mathrm{i}}{\mathrm{2}}{x}^{\mathrm{2}} −{x}\mathrm{ln}\:\left(\mathrm{e}^{\mathrm{2i}{x}} +\mathrm{1}\right)\:+\frac{\mathrm{i}}{\mathrm{2}}\mathrm{L}{i}_{\mathrm{2}} \:\left(−\mathrm{e}^{\mathrm{2i}{x}} \right)\:+{C} \\ $$$$ \\ $$$$\mathrm{hopefully}\:\mathrm{I}\:\mathrm{made}\:\mathrm{no}\:\mathrm{errors},\:\mathrm{please}\:\mathrm{check}! \\ $$
Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{great}\:\mathrm{sir} \\ $$
