Menu Close

calculate-0-1-x-4-1-x-6-dx-

Tinku Tara 0 Comments
Pin




Question Number 33026 by prof Abdo imad last updated on 09/Apr/18
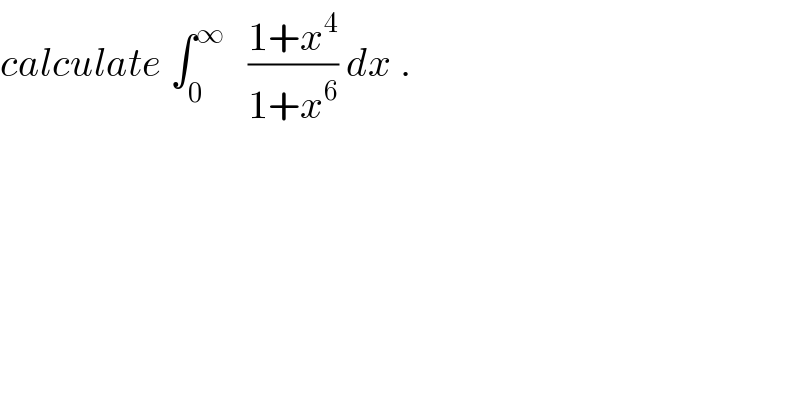
calculate ∫_0 ^∞ ((1+x^4 )/(1+x^6 )) dx .
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}+{x}^{\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{6}} }\:{dx}\:. \\ $$
Commented by abdo imad last updated on 09/Apr/18
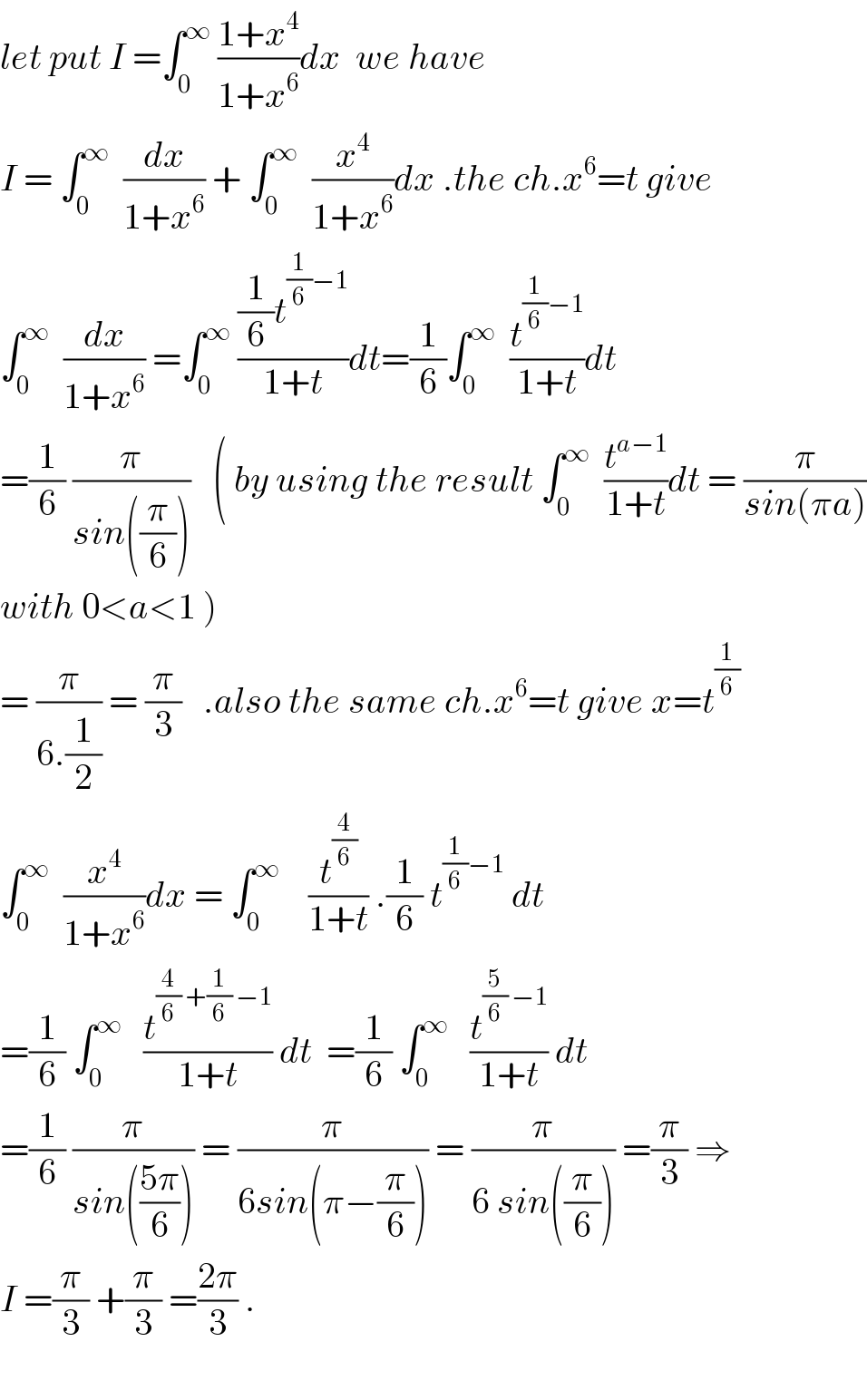
let put I =∫_0 ^∞ ((1+x^4 )/(1+x^6 ))dx we have I = ∫_0 ^∞ (dx/(1+x^6 )) + ∫_0 ^∞ (x^4 /(1+x^6 ))dx .the ch.x^6 =t give ∫_0 ^∞ (dx/(1+x^6 )) =∫_0 ^∞ (((1/6)t^((1/6)−1) )/(1+t))dt=(1/6)∫_0 ^∞ (t^((1/6)−1) /(1+t))dt =(1/6) (π/(sin((π/6)))) ( by using the result ∫_0 ^∞ (t^(a−1) /(1+t))dt = (π/(sin(πa))) with 0<a<1 ) = (π/(6.(1/2))) = (π/3) .also the same ch.x^6 =t give x=t^(1/6) ∫_0 ^∞ (x^4 /(1+x^6 ))dx = ∫_0 ^∞ (t^(4/6) /(1+t)) .(1/6) t^((1/6)−1) dt =(1/6) ∫_0 ^∞ (t^((4/6) +(1/6) −1) /(1+t)) dt =(1/6) ∫_0 ^∞ (t^((5/6) −1) /(1+t)) dt =(1/6) (π/(sin(((5π)/6)))) = (π/(6sin(π−(π/6)))) = (π/(6 sin((π/6)))) =(π/3) ⇒ I =(π/3) +(π/3) =((2π)/3) .
$${let}\:{put}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}+{x}^{\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{6}} }{dx}\:\:{we}\:{have} \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{6}} }\:+\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{6}} }{dx}\:.{the}\:{ch}.{x}^{\mathrm{6}} ={t}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{6}} }\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\frac{\mathrm{1}}{\mathrm{6}}{t}^{\frac{\mathrm{1}}{\mathrm{6}}−\mathrm{1}} }{\mathrm{1}+{t}}{dt}=\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{\frac{\mathrm{1}}{\mathrm{6}}−\mathrm{1}} }{\mathrm{1}+{t}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\:\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{6}}\right)}\:\:\:\left(\:{by}\:{using}\:{the}\:{result}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{{a}−\mathrm{1}} }{\mathrm{1}+{t}}{dt}\:=\:\frac{\pi}{{sin}\left(\pi{a}\right)}\right. \\ $$$$\left.{with}\:\mathrm{0}<{a}<\mathrm{1}\:\right) \\ $$$$=\:\frac{\pi}{\mathrm{6}.\frac{\mathrm{1}}{\mathrm{2}}}\:=\:\frac{\pi}{\mathrm{3}}\:\:\:.{also}\:{the}\:{same}\:{ch}.{x}^{\mathrm{6}} ={t}\:{give}\:{x}={t}^{\frac{\mathrm{1}}{\mathrm{6}}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{6}} }{dx}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{t}^{\frac{\mathrm{4}}{\mathrm{6}}} }{\mathrm{1}+{t}}\:.\frac{\mathrm{1}}{\mathrm{6}}\:{t}^{\frac{\mathrm{1}}{\mathrm{6}}−\mathrm{1}} \:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}^{\frac{\mathrm{4}}{\mathrm{6}}\:+\frac{\mathrm{1}}{\mathrm{6}}\:−\mathrm{1}} }{\mathrm{1}+{t}}\:{dt}\:\:=\frac{\mathrm{1}}{\mathrm{6}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}^{\frac{\mathrm{5}}{\mathrm{6}}\:−\mathrm{1}} }{\mathrm{1}+{t}}\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\:\frac{\pi}{{sin}\left(\frac{\mathrm{5}\pi}{\mathrm{6}}\right)}\:=\:\frac{\pi}{\mathrm{6}{sin}\left(\pi−\frac{\pi}{\mathrm{6}}\right)}\:=\:\frac{\pi}{\mathrm{6}\:{sin}\left(\frac{\pi}{\mathrm{6}}\right)}\:=\frac{\pi}{\mathrm{3}}\:\Rightarrow \\ $$$${I}\:=\frac{\pi}{\mathrm{3}}\:+\frac{\pi}{\mathrm{3}}\:=\frac{\mathrm{2}\pi}{\mathrm{3}}\:. \\ $$$$ \\ $$
Answered by Joel578 last updated on 09/Apr/18
I = lim_(n→∞) (∫_0 ^n ((x^4 + 1)/(x^6 + 1)) dx) ∫ ((x^4 + 1)/(x^6 + 1)) dx = ∫ ((x^4 + 1 + x^2 − x^2 )/((x^2 +1)(x^4 − x^2 + 1))) dx = ∫ (1/(x^2 + 1)) dx + ∫ (x^2 /(x^6 + 1)) dx = tan^(−1) x + ∫ (x^2 /(x^6 + 1)) dx (u = x^3 → du = 3x^2 dx) = tan^(−1) x + (1/3) ∫ (1/(u^2 + 1)) du = tan^(−1) x + (1/3)tan^(−1) u + C = tan^(−1) (x) + (1/3)tan^(−1) (x^3 ) + C I = lim_(n→∞) [tan^(−1) (x) + (1/3)tan^(−1) (x^3 )]_0 ^n = lim_(n→∞) (tan^(−1) (n) + (1/3)tan^(−1) (n^3 )) − (tan^(−1) (0) + (1/3)tan^(−1) (0)) = (π/2) + (1/3)((π/2)) − 0 = ((2π)/3)
$${I}\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\int_{\mathrm{0}} ^{{n}} \:\frac{{x}^{\mathrm{4}} \:+\:\mathrm{1}}{{x}^{\mathrm{6}} \:+\:\mathrm{1}}\:{dx}\right) \\ $$$$ \\ $$$$\int\:\frac{{x}^{\mathrm{4}} \:+\:\mathrm{1}}{{x}^{\mathrm{6}} \:+\:\mathrm{1}}\:{dx}\:=\:\int\:\frac{{x}^{\mathrm{4}} \:+\:\mathrm{1}\:+\:{x}^{\mathrm{2}} \:−\:{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left({x}^{\mathrm{4}} \:−\:{x}^{\mathrm{2}} \:+\:\mathrm{1}\right)}\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\int\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:+\:\mathrm{1}}\:{dx}\:+\:\int\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{6}} \:+\:\mathrm{1}}\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{tan}^{−\mathrm{1}} \:{x}\:+\:\int\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{6}} \:+\:\mathrm{1}}\:{dx}\:\:\:\left({u}\:=\:{x}^{\mathrm{3}} \:\:\rightarrow\:\:{du}\:=\:\mathrm{3}{x}^{\mathrm{2}} \:{dx}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{tan}^{−\mathrm{1}} \:{x}\:+\:\frac{\mathrm{1}}{\mathrm{3}}\:\int\:\frac{\mathrm{1}}{{u}^{\mathrm{2}} \:+\:\mathrm{1}}\:{du} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{tan}^{−\mathrm{1}} \:{x}\:+\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \:{u}\:+\:{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{tan}^{−\mathrm{1}} \:\left({x}\right)\:+\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \:\left({x}^{\mathrm{3}} \right)\:+\:{C} \\ $$$$ \\ $$$${I}\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left[\mathrm{tan}^{−\mathrm{1}} \:\left({x}\right)\:+\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \:\left({x}^{\mathrm{3}} \right)\right]_{\mathrm{0}} ^{{n}} \\ $$$$\:\:\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{tan}^{−\mathrm{1}} \:\left({n}\right)\:+\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \:\left({n}^{\mathrm{3}} \right)\right)\:−\:\left(\mathrm{tan}^{−\mathrm{1}} \:\left(\mathrm{0}\right)\:+\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \:\left(\mathrm{0}\right)\right) \\ $$$$\:\:\:=\:\frac{\pi}{\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\pi}{\mathrm{2}}\right)\:−\:\mathrm{0} \\ $$$$\:\:\:=\:\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *