Question Number 35224 by abdo mathsup 649 cc last updated on 16/May/18
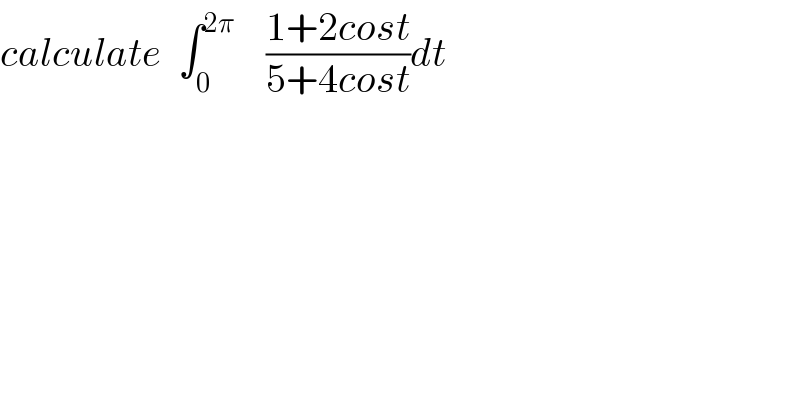
$${calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\:\frac{\mathrm{1}+\mathrm{2}{cost}}{\mathrm{5}+\mathrm{4}{cost}}{dt} \\ $$
Answered by MJS last updated on 17/May/18
![∫((1+2cos t)/(5+4cos t))dt= [((Weierstrass again:)),((u=tan (t/2) → dt=((2du)/(1+u^2 )); t=2arctan u)),((cos t=((1−u^2 )/(1+u^2 )); (sin t=((2u)/(1+u^2 ))))) ] =−2∫((u^2 −3)/((u^2 +1)(u^2 +9)))du= =−2∫(−(1/(2(u^2 +1)))+(3/(2(u^2 +9))))du= =∫(du/(u^2 +1))−3∫(du/(u^2 +9))= [v=(u/3) → du=3dv] =arctan u−3∫(3/(9v^2 +9))dv= =arctan u−∫(dv/(v^2 +1))= =arctan u−arctan v= =arctan u−arctan (u/3)= =arctan(tan (t/2))−arctan ((tan (t/2))/3)= =(t/2)−arctan((1/3)tan (t/2)) ∫_0 ^(2π) ((1+2cos t)/(5+4cos t))dt=π](https://www.tinkutara.com/question/Q35259.png)
$$\int\frac{\mathrm{1}+\mathrm{2cos}\:{t}}{\mathrm{5}+\mathrm{4cos}\:{t}}{dt}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\begin{bmatrix}{\mathrm{Weierstrass}\:\mathrm{again}:}\\{{u}=\mathrm{tan}\:\frac{{t}}{\mathrm{2}}\:\rightarrow\:{dt}=\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} };\:{t}=\mathrm{2arctan}\:{u}}\\{\mathrm{cos}\:{t}=\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} };\:\left(\mathrm{sin}\:{t}=\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }\right)}\end{bmatrix} \\ $$$$=−\mathrm{2}\int\frac{{u}^{\mathrm{2}} −\mathrm{3}}{\left({u}^{\mathrm{2}} +\mathrm{1}\right)\left({u}^{\mathrm{2}} +\mathrm{9}\right)}{du}= \\ $$$$=−\mathrm{2}\int\left(−\frac{\mathrm{1}}{\mathrm{2}\left({u}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{3}}{\mathrm{2}\left({u}^{\mathrm{2}} +\mathrm{9}\right)}\right){du}= \\ $$$$=\int\frac{{du}}{{u}^{\mathrm{2}} +\mathrm{1}}−\mathrm{3}\int\frac{{du}}{{u}^{\mathrm{2}} +\mathrm{9}}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{v}=\frac{{u}}{\mathrm{3}}\:\rightarrow\:{du}=\mathrm{3}{dv}\right] \\ $$$$=\mathrm{arctan}\:{u}−\mathrm{3}\int\frac{\mathrm{3}}{\mathrm{9}{v}^{\mathrm{2}} +\mathrm{9}}{dv}= \\ $$$$=\mathrm{arctan}\:{u}−\int\frac{{dv}}{{v}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$=\mathrm{arctan}\:{u}−\mathrm{arctan}\:{v}= \\ $$$$=\mathrm{arctan}\:{u}−\mathrm{arctan}\:\frac{{u}}{\mathrm{3}}= \\ $$$$=\mathrm{arctan}\left(\mathrm{tan}\:\frac{{t}}{\mathrm{2}}\right)−\mathrm{arctan}\:\frac{\mathrm{tan}\:\frac{{t}}{\mathrm{2}}}{\mathrm{3}}= \\ $$$$=\frac{{t}}{\mathrm{2}}−\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}\:\frac{{t}}{\mathrm{2}}\right) \\ $$$$ \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\frac{\mathrm{1}+\mathrm{2cos}\:{t}}{\mathrm{5}+\mathrm{4cos}\:{t}}{dt}=\pi \\ $$
