Question Number 41054 by turbo msup by abdo last updated on 01/Aug/18
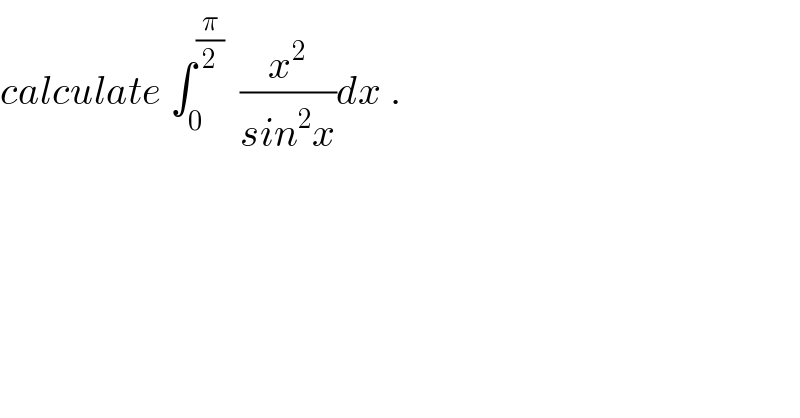
$${calculate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{x}^{\mathrm{2}} }{{sin}^{\mathrm{2}} {x}}{dx}\:. \\ $$
Commented by maxmathsup by imad last updated on 02/Aug/18
![we have cos^2 x =(1/(1+tan^2 x)) ⇒sin^2 x =1−(1/(1+tan^2 x)) =((tan^2 x)/(1+tan^2 x)) ⇒ I = ∫_0 ^(π/2) (x^2 /(sin^2 x)) dx = ∫_0 ^(π/2) (((1+tan^2 x)x^2 )/(tan^2 x)) dx changement tanx =t give I = ∫_0 ^∞ (((1+t^2 ) (arctant)^2 )/t^2 ) (dt/(1+t^2 )) = ∫_0 ^∞ (((arctant)^2 )/t^2 ) dt by parts u^′ =(1/t^2 ) and v =(arctant)^2 ⇒ I =[−(1/t) (arctant)^2 ]_0 ^(+∞) −∫_0 ^∞ −(1/t) ((2arctant)/(1+t^2 ))dt = 2 ∫_0 ^∞ ((arctant)/(t(1+t^2 ))) dt let introduce the parametric function f(x) =∫_0 ^∞ ((arctan(xt))/(t(1+t^2 ))) dt we have f^′ (x) = ∫_0 ^∞ (t/((1+x^2 t^2 )t(1+t^2 )))dt =∫_0 ^∞ (dt/((1+t^2 )(1+x^2 t^2 ))) for x^2 ≠1 we have f^′ (x)= ∫_0 ^∞ (1/(x^2 −1)) ( (1/(1+t^2 )) −(1/(1+x^2 t^2 )))dt = (1/(x^2 −1)) ∫_0 ^∞ (dt/(1+t^2 )) −(1/(x^2 −1)) ∫_0 ^∞ (dt/(1+x^2 t^2 )) but but ∫_0 ^∞ (dt/(1+t^2 )) =(π/2) ∫_0 ^∞ (dt/(1+x^2 t^2 ))dt =_(xt =u) ∫_0 ^∞ (1/(1+u^2 )) (du/x) = (1/x) [arctan(xt)]_0 ^(+∞) ⇒ f^′ (x)= (π/(2(x^2 −1))) −(π/(2x(x^2 −1))) =(π/(2(x^2 −1))){1−(1/x)} =((π(x−1))/(2x(x^2 −1))) = (π/(2x(x+1))) ⇒f(x) = (π/2) ∫_. ^x (dt/(t(t+1))) =(π/2) ∫_. ^x ((1/t)−(1/(t+1)))dt =(π/2)ln∣(x/(x+1))∣ +l we see that l=lim_(x→+∞) f(x) ⇒ f(x) =(π/2)ln∣(x/(x+1))∣ +l ⇒ I =2f(1) =2{(π/2)ln((1/2))+l} =2{−(π/2)ln(2)+l} ⇒ I =2l −πln(2) with l=lim_(x→+∞ ) f(x) .](https://www.tinkutara.com/question/Q41092.png)
$${we}\:{have}\:{cos}^{\mathrm{2}} {x}\:=\frac{\mathrm{1}}{\mathrm{1}+{tan}^{\mathrm{2}} {x}}\:\Rightarrow{sin}^{\mathrm{2}} {x}\:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{tan}^{\mathrm{2}} {x}}\:=\frac{{tan}^{\mathrm{2}} {x}}{\mathrm{1}+{tan}^{\mathrm{2}} {x}}\:\Rightarrow \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{x}^{\mathrm{2}} }{{sin}^{\mathrm{2}} {x}}\:{dx}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right){x}^{\mathrm{2}} }{{tan}^{\mathrm{2}} {x}}\:{dx}\:\:\:{changement}\:{tanx}\:={t}\:{give} \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\:\left({arctant}\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} }\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\left({arctant}\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} }\:{dt}\:{by}\:{parts}\:{u}^{'} \:=\frac{\mathrm{1}}{{t}^{\mathrm{2}} } \\ $$$${and}\:{v}\:=\left({arctant}\right)^{\mathrm{2}} \:\Rightarrow\:{I}\:=\left[−\frac{\mathrm{1}}{{t}}\:\left({arctant}\right)^{\mathrm{2}} \right]_{\mathrm{0}} ^{+\infty} \:−\int_{\mathrm{0}} ^{\infty} \:−\frac{\mathrm{1}}{{t}}\:\frac{\mathrm{2}{arctant}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctant}}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\:{dt}\:{let}\:{introduce}\:{the}\:{parametric}\:{function} \\ $$$${f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({xt}\right)}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\:{dt}\:\:{we}\:{have}\: \\ $$$${f}^{'} \left({x}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{t}}{\left(\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{2}} \right){t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{2}} \right)}\:{for}\:{x}^{\mathrm{2}} \:\neq\mathrm{1}\:{we}\:{have} \\ $$$${f}^{'} \left({x}\right)=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}\:\left(\:\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{2}} }\right){dt}\:=\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{2}} }\:{but} \\ $$$${but}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\frac{\pi}{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{2}} }{dt}\:=_{{xt}\:={u}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\frac{{du}}{{x}}\:=\:\frac{\mathrm{1}}{{x}}\:\left[{arctan}\left({xt}\right)\right]_{\mathrm{0}} ^{+\infty} \:\Rightarrow \\ $$$${f}^{'} \left({x}\right)=\:\frac{\pi}{\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{1}\right)}\:−\frac{\pi}{\mathrm{2}{x}\left({x}^{\mathrm{2}} −\mathrm{1}\right)}\:=\frac{\pi}{\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{1}\right)}\left\{\mathrm{1}−\frac{\mathrm{1}}{{x}}\right\}\:=\frac{\pi\left({x}−\mathrm{1}\right)}{\mathrm{2}{x}\left({x}^{\mathrm{2}} −\mathrm{1}\right)} \\ $$$$=\:\frac{\pi}{\mathrm{2}{x}\left({x}+\mathrm{1}\right)}\:\Rightarrow{f}\left({x}\right)\:=\:\frac{\pi}{\mathrm{2}}\:\int_{.} ^{{x}} \:\frac{{dt}}{{t}\left({t}+\mathrm{1}\right)}\:=\frac{\pi}{\mathrm{2}}\:\int_{.} ^{{x}} \:\left(\frac{\mathrm{1}}{{t}}−\frac{\mathrm{1}}{{t}+\mathrm{1}}\right){dt} \\ $$$$=\frac{\pi}{\mathrm{2}}{ln}\mid\frac{{x}}{{x}+\mathrm{1}}\mid\:+{l}\:{we}\:{see}\:{that}\:{l}={lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)\:\:\Rightarrow \\ $$$${f}\left({x}\right)\:=\frac{\pi}{\mathrm{2}}{ln}\mid\frac{{x}}{{x}+\mathrm{1}}\mid\:+{l}\:\:\Rightarrow\:{I}\:=\mathrm{2}{f}\left(\mathrm{1}\right)\:=\mathrm{2}\left\{\frac{\pi}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+{l}\right\} \\ $$$$=\mathrm{2}\left\{−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)+{l}\right\}\:\Rightarrow\:{I}\:=\mathrm{2}{l}\:−\pi{ln}\left(\mathrm{2}\right)\:{with}\:{l}={lim}_{{x}\rightarrow+\infty\:} {f}\left({x}\right)\:. \\ $$$$ \\ $$$$ \\ $$
