Question Number 36439 by prof Abdo imad last updated on 02/Jun/18
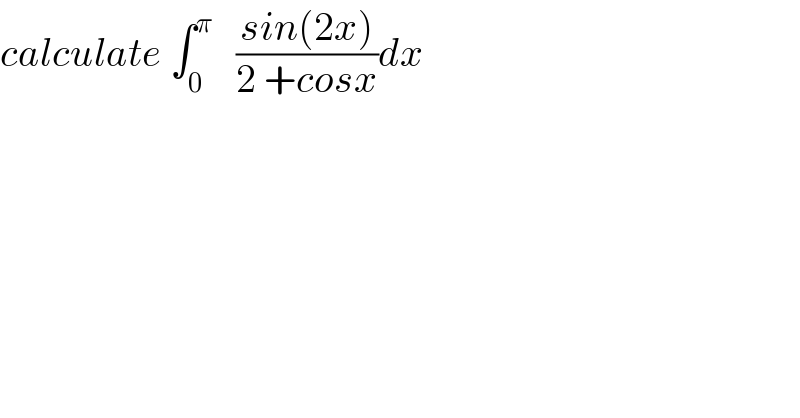
$${calculate}\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{2}\:+{cosx}}{dx} \\ $$
Commented by abdo.msup.com last updated on 03/Jun/18
![I = ∫_0 ^π ((2sinx cosx)/(2+cosx)) dx changement cosx =t give −sinx dx =dt I = ∫_1 ^(−1) ((−2t dt)/(2+t)) =2 ∫_(−1) ^1 (t/(t+2))dt =2 ∫_(−1) ^1 ((t+2 −2)/(t+2))dt =4 −4 [ln∣t+2∣]_(−1) ^1 =4 −4( ln(3)) I =4 −4ln(3) .](https://www.tinkutara.com/question/Q36637.png)
$${I}\:=\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{\mathrm{2}{sinx}\:{cosx}}{\mathrm{2}+{cosx}}\:{dx}\:{changement} \\ $$$${cosx}\:={t}\:{give}\:\:−{sinx}\:{dx}\:={dt} \\ $$$${I}\:=\:\int_{\mathrm{1}} ^{−\mathrm{1}} \:\frac{−\mathrm{2}{t}\:{dt}}{\mathrm{2}+{t}}\:=\mathrm{2}\:\int_{−\mathrm{1}} ^{\mathrm{1}} \:\:\frac{{t}}{{t}+\mathrm{2}}{dt} \\ $$$$=\mathrm{2}\:\int_{−\mathrm{1}} ^{\mathrm{1}} \:\:\frac{{t}+\mathrm{2}\:−\mathrm{2}}{{t}+\mathrm{2}}{dt} \\ $$$$=\mathrm{4}\:\:−\mathrm{4}\:\left[{ln}\mid{t}+\mathrm{2}\mid\right]_{−\mathrm{1}} ^{\mathrm{1}} \\ $$$$=\mathrm{4}\:−\mathrm{4}\left(\:{ln}\left(\mathrm{3}\right)\right) \\ $$$${I}\:=\mathrm{4}\:−\mathrm{4}{ln}\left(\mathrm{3}\right)\:. \\ $$
Answered by ajfour last updated on 02/Jun/18
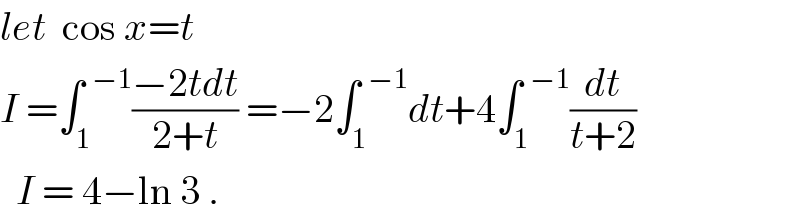
$${let}\:\:\mathrm{cos}\:{x}={t} \\ $$$${I}\:=\int_{\mathrm{1}} ^{\:\:−\mathrm{1}} \frac{−\mathrm{2}{tdt}}{\mathrm{2}+{t}}\:=−\mathrm{2}\int_{\mathrm{1}} ^{\:\:−\mathrm{1}} {dt}+\mathrm{4}\int_{\mathrm{1}} ^{\:\:−\mathrm{1}} \frac{{dt}}{{t}+\mathrm{2}} \\ $$$$\:\:{I}\:=\:\mathrm{4}−\mathrm{ln}\:\mathrm{3}\:. \\ $$
Commented by MJS last updated on 02/Jun/18
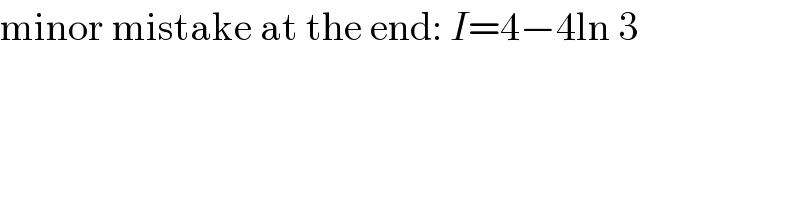
$$\mathrm{minor}\:\mathrm{mistake}\:\mathrm{at}\:\mathrm{the}\:\mathrm{end}:\:{I}=\mathrm{4}−\mathrm{4ln}\:\mathrm{3} \\ $$
