Question Number 57319 by turbo msup by abdo last updated on 02/Apr/19
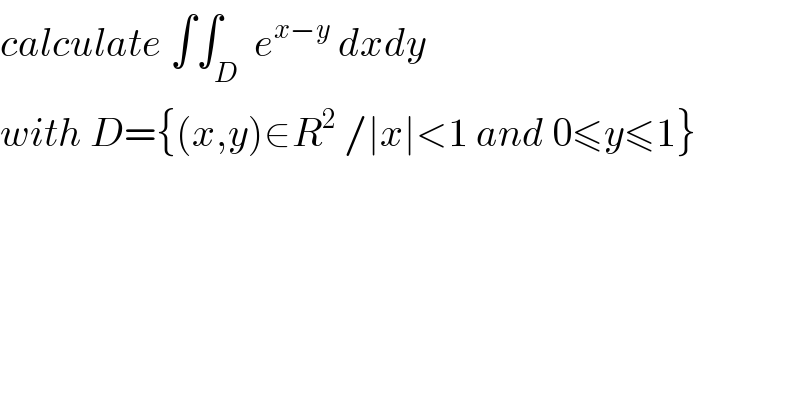
$${calculate}\:\int\int_{{D}} \:{e}^{{x}−{y}} \:{dxdy} \\ $$$${with}\:{D}=\left\{\left({x},{y}\right)\in{R}^{\mathrm{2}} \:/\mid{x}\mid<\mathrm{1}\:{and}\:\mathrm{0}\leqslant{y}\leqslant\mathrm{1}\right\} \\ $$
Commented by maxmathsup by imad last updated on 02/Apr/19
![let I =∫∫_D e^(x−y) dxdy ⇒I =∫_(−1) ^1 e^x dx .∫_0 ^1 e^(−y) dy =[e^x ]_(−1) ^1 .[−e^(−y) ]_0 ^1 =(e−e^(−1) )(1−e^(−1) ) =e−1−e^(−1) +e^(−2) ⇒I =e−1−(1/e) +(1/e^2 ) .](https://www.tinkutara.com/question/Q57342.png)
$${let}\:{I}\:=\int\int_{{D}} {e}^{{x}−{y}} {dxdy}\:\Rightarrow{I}\:=\int_{−\mathrm{1}} ^{\mathrm{1}} \:{e}^{{x}} \:{dx}\:.\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−{y}} {dy} \\ $$$$=\left[{e}^{{x}} \right]_{−\mathrm{1}} ^{\mathrm{1}} \:.\left[−{e}^{−{y}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:=\left({e}−{e}^{−\mathrm{1}} \right)\left(\mathrm{1}−{e}^{−\mathrm{1}} \right)\:={e}−\mathrm{1}−{e}^{−\mathrm{1}} \:+{e}^{−\mathrm{2}} \\ $$$$\Rightarrow{I}\:={e}−\mathrm{1}−\frac{\mathrm{1}}{{e}}\:+\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\:. \\ $$
Answered by kaivan.ahmadi last updated on 02/Apr/19
![∫_0 ^1 ∫_(−1) ^1 e^(x−y) dxdy=∫_0 ^1 e^(x−y) ∣_(−1) ^1 dy= ∫_0 ^1 (e^(1−y) −e^(−1−y) )dy= −e^(1−y) +e^(−1−y) ∣_0 ^1 =[−1+e^(−2) ]−[−e+e^(−1) ]= −1+(1/e^2 )+e−(1/e)=((−e^2 +1+e^3 −e)/e^2 )](https://www.tinkutara.com/question/Q57322.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \int_{−\mathrm{1}} ^{\mathrm{1}} {e}^{{x}−{y}} {dxdy}=\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{{x}−{y}} \mid_{−\mathrm{1}} ^{\mathrm{1}} {dy}= \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left({e}^{\mathrm{1}−{y}} −{e}^{−\mathrm{1}−{y}} \right){dy}= \\ $$$$−{e}^{\mathrm{1}−{y}} +{e}^{−\mathrm{1}−{y}} \mid_{\mathrm{0}} ^{\mathrm{1}} =\left[−\mathrm{1}+{e}^{−\mathrm{2}} \right]−\left[−{e}+{e}^{−\mathrm{1}} \right]= \\ $$$$−\mathrm{1}+\frac{\mathrm{1}}{{e}^{\mathrm{2}} }+{e}−\frac{\mathrm{1}}{{e}}=\frac{−{e}^{\mathrm{2}} +\mathrm{1}+{e}^{\mathrm{3}} −{e}}{{e}^{\mathrm{2}} } \\ $$
