Question Number 61045 by mathsolverby Abdo last updated on 28/May/19

$${calculate}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:{cos}\left(\mathrm{2}{arctanx}\right){dx} \\ $$$${and}\:{J}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:{sin}\left(\mathrm{2}{arctanx}\right){dx} \\ $$
Commented by maxmathsup by imad last updated on 29/May/19
![we have cos(2u) =2cos^2 (u)−1 ⇒cos(2arctan(x))=2cos^2 (arctanx)−1 =2((1/( (√(1+x^2 )))))^2 −1 =(2/(1+x^2 )) −1 ⇒ I =∫_0 ^1 ((2/(1+x^2 )) −1)dx =2∫_0 ^1 (dx/(1+x^2 )) −1 =2 [arctan(x)]_0 ^1 −1 =2(π/4)−1 =(π/2)−1](https://www.tinkutara.com/question/Q61102.png)
$${we}\:{have}\:{cos}\left(\mathrm{2}{u}\right)\:=\mathrm{2}{cos}^{\mathrm{2}} \left({u}\right)−\mathrm{1}\:\Rightarrow{cos}\left(\mathrm{2}{arctan}\left({x}\right)\right)=\mathrm{2}{cos}^{\mathrm{2}} \left({arctanx}\right)−\mathrm{1} \\ $$$$=\mathrm{2}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)^{\mathrm{2}} −\mathrm{1}\:=\frac{\mathrm{2}}{\mathrm{1}+{x}^{\mathrm{2}} }\:−\mathrm{1}\:\Rightarrow\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{1}+{x}^{\mathrm{2}} }\:−\mathrm{1}\right){dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:−\mathrm{1}\:=\mathrm{2}\:\left[{arctan}\left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{1}\:=\mathrm{2}\frac{\pi}{\mathrm{4}}−\mathrm{1}\:=\frac{\pi}{\mathrm{2}}−\mathrm{1} \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 29/May/19
![let J =∫_0 ^1 sin(2arctanx)dx we have sin(2x) =2sinx cosx ⇒ sin(2arctanx) =2sin(arctanx)cos(arctanx) =2 (x/( (√(1+x^2 )))) (1/( (√(1+x^2 )))) =((2x)/(1+x^2 )) ⇒J =∫_0 ^1 ((2x)/(1+x^2 ))dx =[ln(1+x^2 )]_0 ^1 =ln(2) .](https://www.tinkutara.com/question/Q61103.png)
$${let}\:{J}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:{sin}\left(\mathrm{2}{arctanx}\right){dx}\:\:\:{we}\:{have}\:{sin}\left(\mathrm{2}{x}\right)\:=\mathrm{2}{sinx}\:{cosx}\:\Rightarrow \\ $$$${sin}\left(\mathrm{2}{arctanx}\right)\:=\mathrm{2}{sin}\left({arctanx}\right){cos}\left({arctanx}\right) \\ $$$$=\mathrm{2}\:\frac{{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:=\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\Rightarrow{J}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:=\left[{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$={ln}\left(\mathrm{2}\right)\:. \\ $$
Answered by perlman last updated on 28/May/19
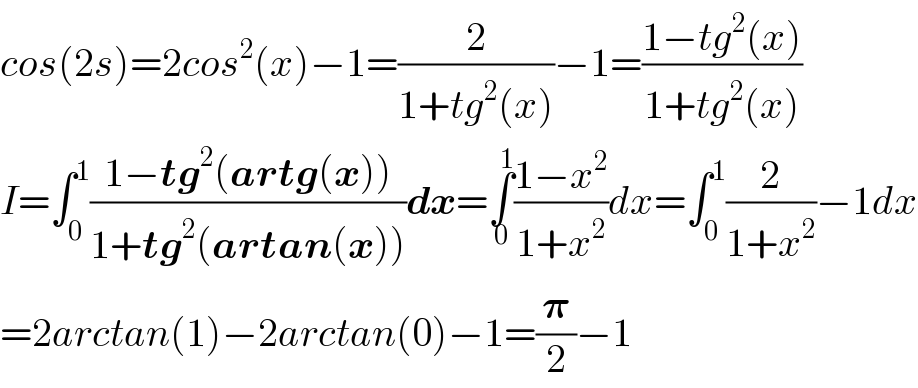
$${cos}\left(\mathrm{2}{s}\right)=\mathrm{2}{cos}^{\mathrm{2}} \left({x}\right)−\mathrm{1}=\frac{\mathrm{2}}{\mathrm{1}+{tg}^{\mathrm{2}} \left({x}\right)}−\mathrm{1}=\frac{\mathrm{1}−{tg}^{\mathrm{2}} \left({x}\right)}{\mathrm{1}+{tg}^{\mathrm{2}} \left({x}\right)} \\ $$$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−\boldsymbol{{tg}}^{\mathrm{2}} \left(\boldsymbol{{artg}}\left(\boldsymbol{{x}}\right)\right)}{\mathrm{1}+\boldsymbol{{tg}}^{\mathrm{2}} \left(\boldsymbol{{artan}}\left(\boldsymbol{{x}}\right)\right)}\boldsymbol{{dx}}=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}}{\mathrm{1}+{x}^{\mathrm{2}} }−\mathrm{1}{dx} \\ $$$$=\mathrm{2}{arctan}\left(\mathrm{1}\right)−\mathrm{2}{arctan}\left(\mathrm{0}\right)−\mathrm{1}=\frac{\boldsymbol{\pi}}{\mathrm{2}}−\mathrm{1} \\ $$
Commented by maxmathsup by imad last updated on 29/May/19
$${where}\:{are}\:{you}\:{from}\:{sir}\:… \\ $$
Commented by perlman last updated on 29/May/19

$${FRANCE} \\ $$
Commented by Mr X pcx last updated on 29/May/19
$${you}\:{are}\:{welcome}\:{sir}\:{glad}\:{to}\:{know}\:{you} \\ $$$${i}\:{have}\:{lots}\:{of}\:{my}\:\:{relatives}\:{in}\:{france} \\ $$$${and}\:{italy}… \\ $$$$ \\ $$
Answered by perlman last updated on 28/May/19
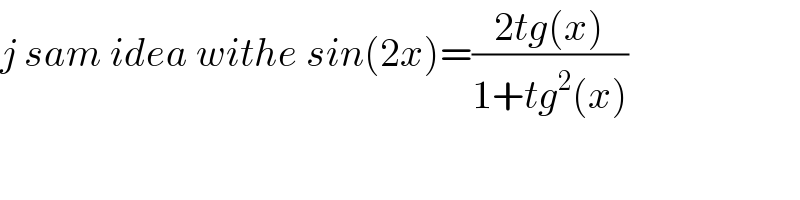
$${j}\:{sam}\:{idea}\:{withe}\:{sin}\left(\mathrm{2}{x}\right)=\frac{\mathrm{2}{tg}\left({x}\right)}{\mathrm{1}+{tg}^{\mathrm{2}} \left({x}\right)} \\ $$
