Question Number 42489 by maxmathsup by imad last updated on 26/Aug/18
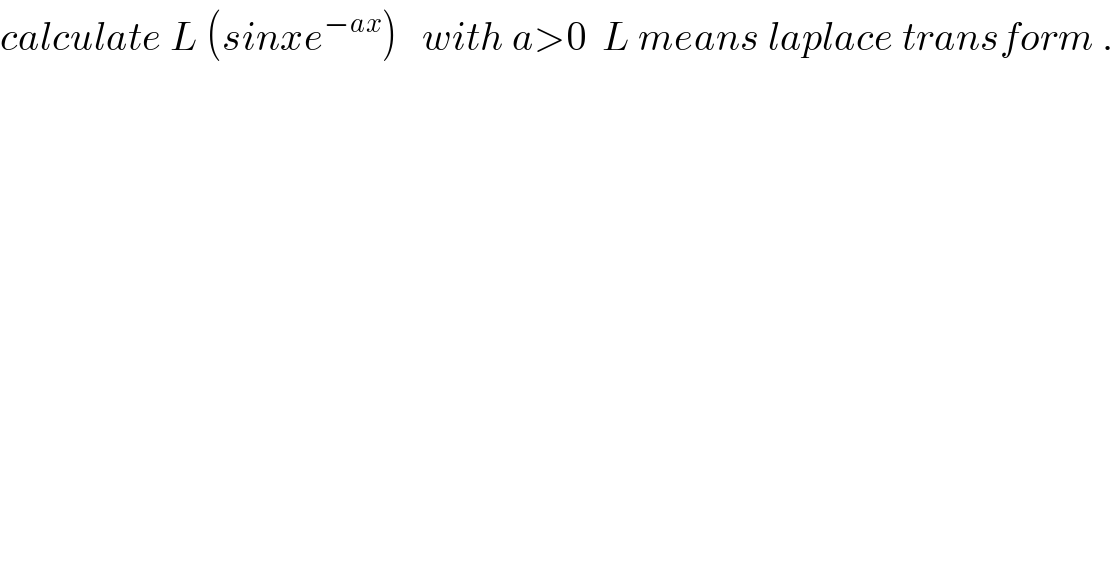
$${calculate}\:{L}\:\left({sinxe}^{−{ax}} \right)\:\:\:{with}\:{a}>\mathrm{0}\:\:{L}\:{means}\:{laplace}\:{transform}\:. \\ $$
Commented by maxmathsup by imad last updated on 27/Aug/18
![L(sinx e^(−ax) )=∫_0 ^∞ sint e^(−at) e^(−xt) dt =L(f)(x) = ∫_0 ^∞ sint e^(−(a+x)t) dt =Im (∫_0 ^∞ e^(it −(a+x)t) dt) but ∫_0 ^∞ e^((i−a−x)t) dt = [(1/(i−a−x)) e^((i−a−x)t) ]_(t=0) ^(+∞) =(1/(i−a−x))(−1) =(1/(a+x −i)) =((a+x+i)/((a+x)^2 +1)) ⇒ L(sinx e^(−ax) ) = (1/((a+x)^2 +1)) .](https://www.tinkutara.com/question/Q42555.png)
$${L}\left({sinx}\:{e}^{−{ax}} \right)=\int_{\mathrm{0}} ^{\infty} \:\:{sint}\:{e}^{−{at}} \:{e}^{−{xt}} \:{dt}\:={L}\left({f}\right)\left({x}\right) \\ $$$$=\:\int_{\mathrm{0}} ^{\infty} \:\:{sint}\:{e}^{−\left({a}+{x}\right){t}} \:{dt}\:={Im}\:\left(\int_{\mathrm{0}} ^{\infty} \:\:{e}^{{it}\:−\left({a}+{x}\right){t}} {dt}\right)\:\:{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\:{e}^{\left({i}−{a}−{x}\right){t}} {dt}\:=\:\left[\frac{\mathrm{1}}{{i}−{a}−{x}}\:{e}^{\left({i}−{a}−{x}\right){t}} \right]_{{t}=\mathrm{0}} ^{+\infty} \:=\frac{\mathrm{1}}{{i}−{a}−{x}}\left(−\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{{a}+{x}\:−{i}}\:=\frac{{a}+{x}+{i}}{\left({a}+{x}\right)^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\:{L}\left({sinx}\:{e}^{−{ax}} \right)\:=\:\frac{\mathrm{1}}{\left({a}+{x}\right)^{\mathrm{2}} \:+\mathrm{1}}\:. \\ $$
