Question Number 162424 by mnjuly1970 last updated on 29/Dec/21
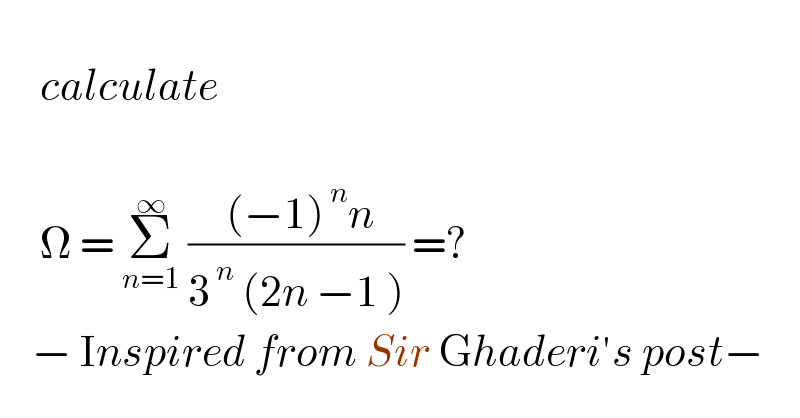
$$ \\ $$$$\:\:\:\:\:{calculate}\: \\ $$$$ \\ $$$$\:\:\:\:\:\Omega\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\:\left(−\mathrm{1}\right)^{\:{n}} {n}}{\mathrm{3}^{\:{n}} \:\left(\mathrm{2}{n}\:−\mathrm{1}\:\right)}\:=?\:\:\:\: \\ $$$$\:\:\:\:−\:\mathrm{I}{nspired}\:{from}\:{Sir}\:\mathrm{G}{haderi}'{s}\:{post}− \\ $$
Answered by Ar Brandon last updated on 29/Dec/21
![Ω=Σ_(n=1) ^∞ (((−1)^n n)/(3^n (2n−1)))=(1/2)Σ_(n=1) ^∞ (−(1/3))^n +(1/2)Σ_(n=1) ^∞ (−(1/3))^n (1/(2n−1)) =−(1/8)+(1/2)Σ_(n=1) ^∞ (−(1/3))^n ∫_0 ^1 x^(2n−2) dx=−(1/8)+(1/2)∫_0 ^1 (1/x^2 )Σ_(n=1) ^∞ (−(x^2 /3))^n dx =−(1/8)−(1/2)∫_0 ^1 (1/x^2 )∙((x^2 /3)/(1+(x^2 /3)))dx=−(1/8)−(1/2)∫_0 ^1 (1/(x^2 +3))dx =−(1/8)−[(1/(2(√3)))arctan((x/( (√3))))]_0 ^1 =−(1/8)−(π/(12(√3)))](https://www.tinkutara.com/question/Q162434.png)
$$\Omega=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {n}}{\mathrm{3}^{{n}} \left(\mathrm{2}{n}−\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\frac{\mathrm{1}}{\mathrm{3}}\right)^{{n}} +\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\frac{\mathrm{1}}{\mathrm{3}}\right)^{{n}} \frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}} \\ $$$$\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\frac{\mathrm{1}}{\mathrm{3}}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}{n}−\mathrm{2}} {dx}=−\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} }\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\frac{{x}^{\mathrm{2}} }{\mathrm{3}}\right)^{{n}} {dx} \\ $$$$\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} }\centerdot\frac{\frac{{x}^{\mathrm{2}} }{\mathrm{3}}}{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}}{dx}=−\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{3}}{dx} \\ $$$$\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{8}}−\left[\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\frac{{x}}{\:\sqrt{\mathrm{3}}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{8}}−\frac{\pi}{\mathrm{12}\sqrt{\mathrm{3}}} \\ $$
Commented by mnjuly1970 last updated on 29/Dec/21
$$\:\:\:\:{thank}\:{you}\:{so}\:{much}\:{sir}\:{brandon} \\ $$
Commented by Ar Brandon last updated on 29/Dec/21

$$\mathrm{My}\:\mathrm{pleasure},\:\mathrm{Sir}\:! \\ $$
