Question Number 61662 by maxmathsup by imad last updated on 06/Jun/19
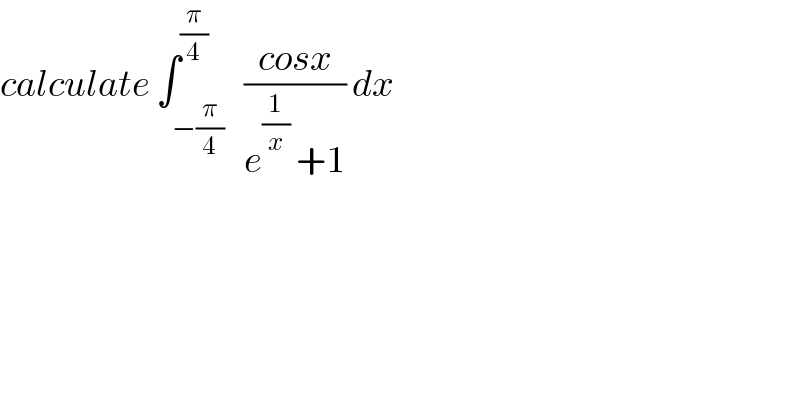
$${calculate}\:\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{cosx}}{{e}^{\frac{\mathrm{1}}{{x}}} \:+\mathrm{1}}\:{dx}\: \\ $$
Commented by maxmathsup by imad last updated on 07/Jun/19
![let f(x) =((cosx)/(e^(1/x) +1)) we have the decomposition f(x)=((f(x)+f(−x))/2)(even) +((f(x)−f(−x))/2) (odd) ⇒ I =∫_(−(π/4)) ^(π/4) ((f(x)+f(−x))/2)dx + ∫_(−(π/4)) ^(π/4) ((f(x)−f(−x))/2)dx =H +K K =0 ⇒ I = ∫_0 ^(π/4) {((cos(x))/(e^(1/x) +1)) +((cosx)/(e^(−(1/x)) +1))}dx=∫_0 ^(π/4) {((e^(−(1/x)) +1 +e^(1/x) +1)/(1 +e^(1/x) +e^(−(1/x)) +1))}cosxdx = ∫_0 ^(π/4) cos(x)dx =[sinx]_0 ^(π/4) =((√2)/2) ⇒ I =((√2)/2) .](https://www.tinkutara.com/question/Q61732.png)
$${let}\:{f}\left({x}\right)\:=\frac{{cosx}}{{e}^{\frac{\mathrm{1}}{{x}}} \:+\mathrm{1}}\:\:{we}\:{have}\:{the}\:{decomposition}\:{f}\left({x}\right)=\frac{{f}\left({x}\right)+{f}\left(−{x}\right)}{\mathrm{2}}\left({even}\right)\:+\frac{{f}\left({x}\right)−{f}\left(−{x}\right)}{\mathrm{2}}\:\left({odd}\right) \\ $$$$\Rightarrow\:{I}\:=\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{f}\left({x}\right)+{f}\left(−{x}\right)}{\mathrm{2}}{dx}\:+\:\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{{f}\left({x}\right)−{f}\left(−{x}\right)}{\mathrm{2}}{dx}\:={H}\:+{K} \\ $$$${K}\:=\mathrm{0}\:\Rightarrow\:{I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left\{\frac{{cos}\left({x}\right)}{{e}^{\frac{\mathrm{1}}{{x}}} +\mathrm{1}}\:+\frac{{cosx}}{{e}^{−\frac{\mathrm{1}}{{x}}} \:+\mathrm{1}}\right\}{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\left\{\frac{{e}^{−\frac{\mathrm{1}}{{x}}} \:+\mathrm{1}\:+{e}^{\frac{\mathrm{1}}{{x}}} \:+\mathrm{1}}{\mathrm{1}\:+{e}^{\frac{\mathrm{1}}{{x}}} \:+{e}^{−\frac{\mathrm{1}}{{x}}} \:+\mathrm{1}}\right\}{cosxdx} \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}\left({x}\right){dx}\:=\left[{sinx}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\:\Rightarrow\:\:{I}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:. \\ $$
