Question Number 128582 by john_santu last updated on 08/Jan/21
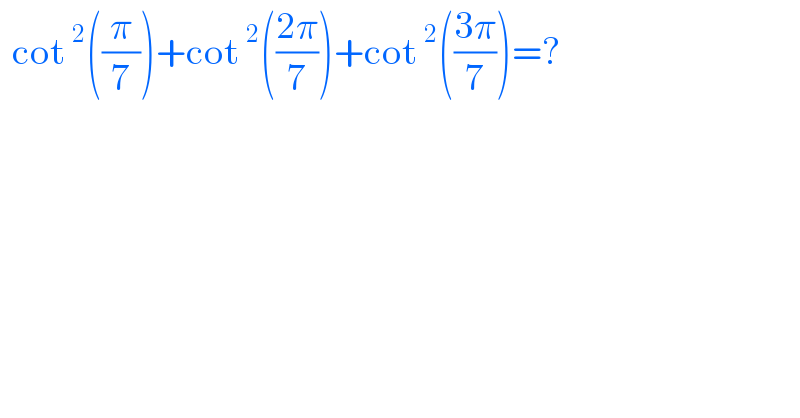
$$\:\:\mathrm{cot}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{7}}\right)+\mathrm{cot}\:^{\mathrm{2}} \left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)+\mathrm{cot}\:^{\mathrm{2}} \left(\frac{\mathrm{3}\pi}{\mathrm{7}}\right)=? \\ $$
Answered by liberty last updated on 08/Jan/21
![T = cot^2 ((π/7))+cot^2 (((2π)/7))+cot^2 (((3π)/7)) T=csc^2 ((π/7))+csc^2 (((2π)/7))+csc^2 (((3π)/7))−3 T= (1/(sin^2 ((π/7))))+(1/(sin^2 (((2π)/7))))+(1/(sin^2 (((3π)/7))))−3 T = (2/(1−cos (((2π)/7))))+(2/(1−cos (((4π)/7))))+(2/(1−cos (((6π)/7))))−3 T= (2/(1+cos ((π/7))))+(2/(1+cos (((3π)/7))))+(2/(1+cos (((5π)/7))))−3 T= ((2 [ (1+cos (π/7))(1+cos ((3π)/7))+(1+cos (π/7))(1+cos ((5π)/7))+(1+cos ((3π)/7))(1+cos ((5π)/7)) ])/((1+cos (π/7))(1+cos ((3π)/7))(1+cos ((5π)/7))))−3 T= ((2[1+cos (π/7)+cos ((3π)/7)+cos (π/7).cos ((3π)/7)+1+cos (π/7)+cos ((5π)/7)+cos (π/7).cos ((5π)/7)+1+cos ((3π)/7)+cos ((5π)/7)+cos ((3π)/7).cos ((5π)/7) ])/((1+cos ((5π)/7))(1+cos (π/7)+cos ((3π)/7)+cos (π/7).cos ((3π)/7))))−3 T = 8−3 = 5](https://www.tinkutara.com/question/Q128584.png)
$$\:\mathrm{T}\:=\:\mathrm{cot}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{7}}\right)+\mathrm{cot}\:^{\mathrm{2}} \left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)+\mathrm{cot}\:^{\mathrm{2}} \left(\frac{\mathrm{3}\pi}{\mathrm{7}}\right) \\ $$$$\:\mathrm{T}=\mathrm{csc}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{7}}\right)+\mathrm{csc}^{\mathrm{2}} \left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)+\mathrm{csc}^{\mathrm{2}} \left(\frac{\mathrm{3}\pi}{\mathrm{7}}\right)−\mathrm{3} \\ $$$$\:\mathrm{T}=\:\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{7}}\right)}+\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)}+\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{3}\pi}{\mathrm{7}}\right)}−\mathrm{3} \\ $$$$\:\mathrm{T}\:=\:\frac{\mathrm{2}}{\mathrm{1}−\mathrm{cos}\:\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)}+\frac{\mathrm{2}}{\mathrm{1}−\mathrm{cos}\:\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right)}+\frac{\mathrm{2}}{\mathrm{1}−\mathrm{cos}\:\left(\frac{\mathrm{6}\pi}{\mathrm{7}}\right)}−\mathrm{3} \\ $$$$\:\mathrm{T}=\:\frac{\mathrm{2}}{\mathrm{1}+\mathrm{cos}\:\left(\frac{\pi}{\mathrm{7}}\right)}+\frac{\mathrm{2}}{\mathrm{1}+\mathrm{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{7}}\right)}+\frac{\mathrm{2}}{\mathrm{1}+\mathrm{cos}\:\left(\frac{\mathrm{5}\pi}{\mathrm{7}}\right)}−\mathrm{3} \\ $$$$\:\mathrm{T}=\:\frac{\mathrm{2}\:\left[\:\left(\mathrm{1}+\mathrm{cos}\:\frac{\pi}{\mathrm{7}}\right)\left(\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{7}}\right)+\left(\mathrm{1}+\mathrm{cos}\:\frac{\pi}{\mathrm{7}}\right)\left(\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{7}}\right)+\left(\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{7}}\right)\left(\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{7}}\right)\:\right]}{\left(\mathrm{1}+\mathrm{cos}\:\frac{\pi}{\mathrm{7}}\right)\left(\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{7}}\right)\left(\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{7}}\right)}−\mathrm{3} \\ $$$$\:\mathrm{T}=\:\frac{\mathrm{2}\left[\mathrm{1}+\mathrm{cos}\:\frac{\pi}{\mathrm{7}}+\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{7}}+\mathrm{cos}\:\frac{\pi}{\mathrm{7}}.\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{7}}+\mathrm{1}+\mathrm{cos}\:\frac{\pi}{\mathrm{7}}+\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{7}}+\mathrm{cos}\:\frac{\pi}{\mathrm{7}}.\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{7}}+\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{7}}+\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{7}}+\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{7}}.\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{7}}\:\right]}{\left(\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{7}}\right)\left(\mathrm{1}+\mathrm{cos}\:\frac{\pi}{\mathrm{7}}+\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{7}}+\mathrm{cos}\:\frac{\pi}{\mathrm{7}}.\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{7}}\right)}−\mathrm{3} \\ $$$$\mathrm{T}\:=\:\mathrm{8}−\mathrm{3}\:=\:\mathrm{5}\: \\ $$
Commented by Study last updated on 10/Jan/21
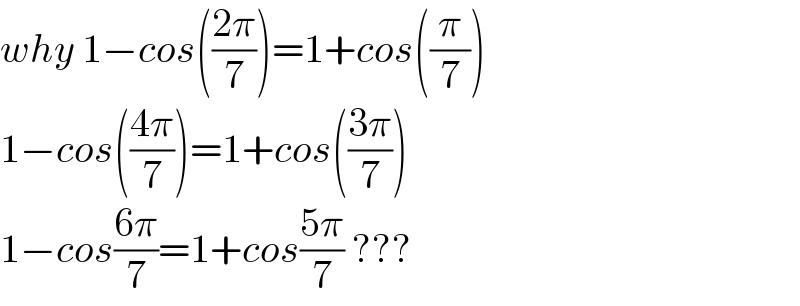
$${why}\:\mathrm{1}−{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)=\mathrm{1}+{cos}\left(\frac{\pi}{\mathrm{7}}\right) \\ $$$$\mathrm{1}−{cos}\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right)=\mathrm{1}+{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{7}}\right) \\ $$$$\mathrm{1}−{cos}\frac{\mathrm{6}\pi}{\mathrm{7}}=\mathrm{1}+{cos}\frac{\mathrm{5}\pi}{\mathrm{7}}\:??? \\ $$
Commented by liberty last updated on 13/Jan/21
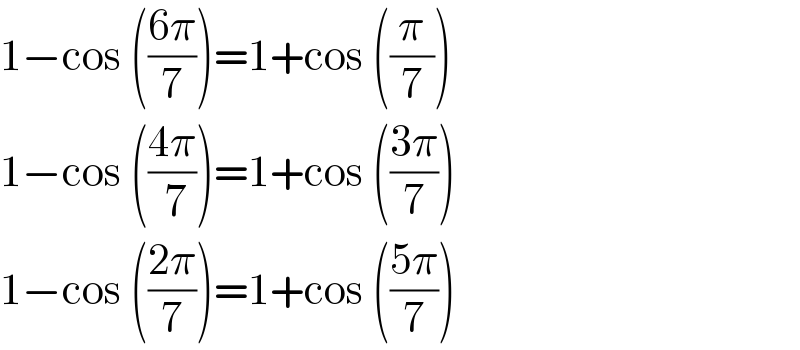
$$\mathrm{1}−\mathrm{cos}\:\left(\frac{\mathrm{6}\pi}{\mathrm{7}}\right)=\mathrm{1}+\mathrm{cos}\:\left(\frac{\pi}{\mathrm{7}}\right) \\ $$$$\mathrm{1}−\mathrm{cos}\:\left(\frac{\mathrm{4}\pi}{\:\mathrm{7}}\right)=\mathrm{1}+\mathrm{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{7}}\right) \\ $$$$\mathrm{1}−\mathrm{cos}\:\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)=\mathrm{1}+\mathrm{cos}\:\left(\frac{\mathrm{5}\pi}{\mathrm{7}}\right) \\ $$
Commented by Adel last updated on 14/Jan/21

$$ \\ $$Please help improve this article or section by expanding it
Commented by Adel last updated on 14/Jan/21
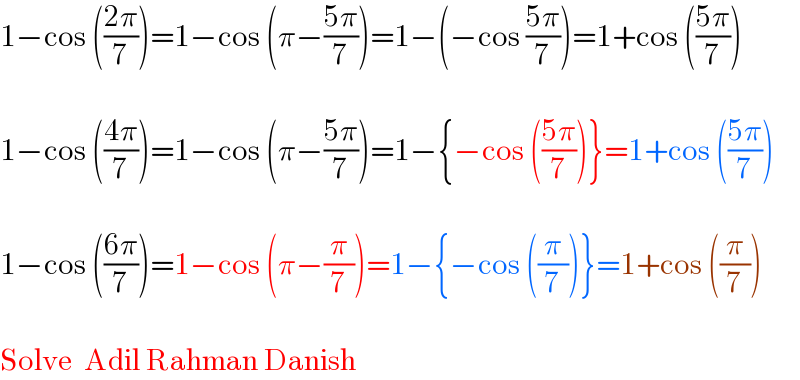
$$\mathrm{1}−\mathrm{cos}\:\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)=\mathrm{1}−\mathrm{cos}\:\left(\pi−\frac{\mathrm{5}\pi}{\mathrm{7}}\right)=\mathrm{1}−\left(−\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{7}}\right)=\mathrm{1}+\mathrm{cos}\:\left(\frac{\mathrm{5}\pi}{\mathrm{7}}\right) \\ $$$$ \\ $$$$\mathrm{1}−\mathrm{cos}\:\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right)=\mathrm{1}−\mathrm{cos}\:\left(\pi−\frac{\mathrm{5}\pi}{\mathrm{7}}\right)=\mathrm{1}−\left\{−\mathrm{cos}\:\left(\frac{\mathrm{5}\pi}{\mathrm{7}}\right)\right\}=\mathrm{1}+\mathrm{cos}\:\left(\frac{\mathrm{5}\pi}{\mathrm{7}}\right) \\ $$$$ \\ $$$$\mathrm{1}−\mathrm{cos}\:\left(\frac{\mathrm{6}\pi}{\mathrm{7}}\right)=\mathrm{1}−\mathrm{cos}\:\left(\pi−\frac{\pi}{\mathrm{7}}\right)=\mathrm{1}−\left\{−\mathrm{cos}\:\left(\frac{\pi}{\mathrm{7}}\right)\right\}=\mathrm{1}+\mathrm{cos}\:\left(\frac{\pi}{\mathrm{7}}\right) \\ $$$$ \\ $$$$\mathrm{Solve}\:\:\mathrm{Adil}\:\mathrm{Rahman}\:\mathrm{Danish} \\ $$
