Question Number 119784 by bemath last updated on 27/Oct/20
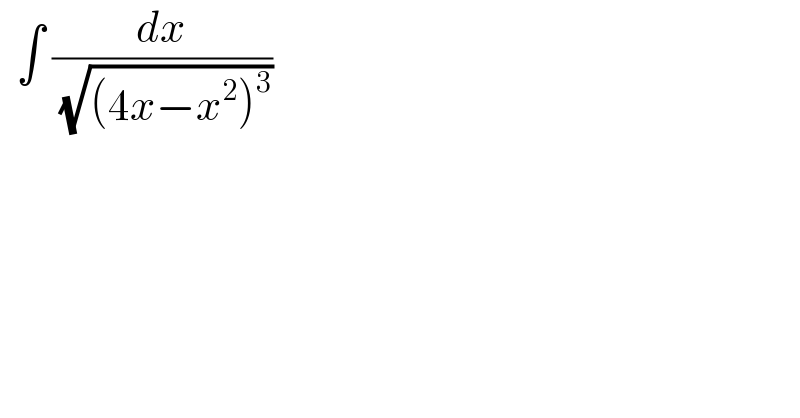
$$\:\:\int\:\frac{{dx}}{\:\sqrt{\left(\mathrm{4}{x}−{x}^{\mathrm{2}} \right)^{\mathrm{3}} }} \\ $$$$ \\ $$
Answered by bobhans last updated on 27/Oct/20
![∫ (dx/( (4−(2−x)^2 )^(3/2) )) ; [ let 2−x = 2sin t ] dx = −2cos t dt ] ∫ ((−2cos t dt)/((4−4sin^2 t)^(3/2) )) = ∫ ((−cos t dt)/(4cos^3 t)) =−(1/4)∫ (1/(cos^2 t)) dt = −(1/4)tan t + c =−((2−x)/(4(√(4x−x^2 )))) + c = ((x−2)/(4(√(4x−x^2 )))) + c](https://www.tinkutara.com/question/Q119788.png)
$$\int\:\frac{{dx}}{\:\left(\mathrm{4}−\left(\mathrm{2}−{x}\right)^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:;\:\left[\:{let}\:\mathrm{2}−{x}\:=\:\mathrm{2sin}\:{t}\:\right]\: \\ $$$$\left.{dx}\:=\:−\mathrm{2cos}\:{t}\:{dt}\:\right] \\ $$$$\int\:\frac{−\mathrm{2cos}\:{t}\:{dt}}{\left(\mathrm{4}−\mathrm{4sin}\:^{\mathrm{2}} {t}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:=\:\int\:\frac{−\mathrm{cos}\:{t}\:{dt}}{\mathrm{4cos}\:^{\mathrm{3}} {t}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\int\:\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} {t}}\:{dt}\:=\:−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{tan}\:{t}\:+\:{c}\: \\ $$$$=−\frac{\mathrm{2}−{x}}{\mathrm{4}\sqrt{\mathrm{4}{x}−{x}^{\mathrm{2}} }}\:+\:{c}\:=\:\frac{{x}−\mathrm{2}}{\mathrm{4}\sqrt{\mathrm{4}{x}−{x}^{\mathrm{2}} }}\:+\:{c} \\ $$
Answered by MJS_new last updated on 28/Oct/20
![∫(dx/(x^(3/2) (4−x)^(3/2) ))= [t=((√x)/( (√(4−x)))) → dx=((√(x(4−x)^3 ))/2)dt] =(1/8)∫1+(1/t^2 )dt=(t/8)−(1/(8t))=((x−2)/(4(√(x(4−x)))))+C](https://www.tinkutara.com/question/Q119988.png)
$$\int\frac{{dx}}{{x}^{\mathrm{3}/\mathrm{2}} \left(\mathrm{4}−{x}\right)^{\mathrm{3}/\mathrm{2}} }= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt{{x}}}{\:\sqrt{\mathrm{4}−{x}}}\:\rightarrow\:{dx}=\frac{\sqrt{{x}\left(\mathrm{4}−{x}\right)^{\mathrm{3}} }}{\mathrm{2}}{dt}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }{dt}=\frac{{t}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{8}{t}}=\frac{{x}−\mathrm{2}}{\mathrm{4}\sqrt{{x}\left(\mathrm{4}−{x}\right)}}+{C} \\ $$
