Question Number 127743 by arash sharifi last updated on 01/Jan/21
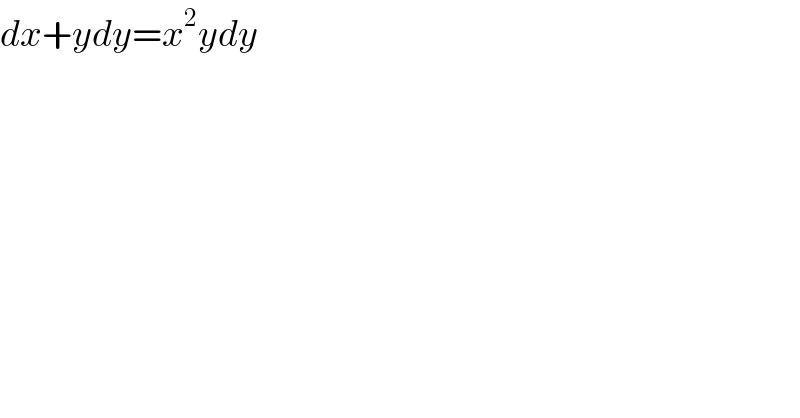
$${dx}+{ydy}={x}^{\mathrm{2}} {ydy} \\ $$
Commented by mr W last updated on 01/Jan/21
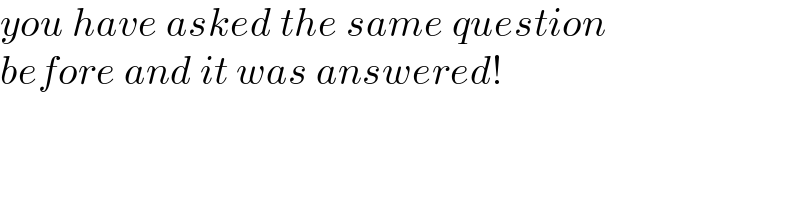
$${you}\:{have}\:{asked}\:{the}\:{same}\:{question}\: \\ $$$${before}\:{and}\:{it}\:{was}\:{answered}! \\ $$
Answered by Olaf last updated on 01/Jan/21
![dx+ydx = x^2 ydy dx = y(x^2 −1)dy (dx/(x^2 −1)) = ydy (1/2)[(1/(x−1))−(1/(x+1))]dx = ydy (1/2)ln∣((x−1)/(x+1))∣ = (1/2)y^2 +C_1 y = ±(√(ln∣((x−1)/(x+1))∣+C_2 ))](https://www.tinkutara.com/question/Q127751.png)
$${dx}+{ydx}\:=\:{x}^{\mathrm{2}} {ydy} \\ $$$${dx}\:=\:{y}\left({x}^{\mathrm{2}} −\mathrm{1}\right){dy} \\ $$$$\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{1}}\:=\:{ydy} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{{x}−\mathrm{1}}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right]{dx}\:=\:{ydy} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\mid\:=\:\frac{\mathrm{1}}{\mathrm{2}}{y}^{\mathrm{2}} +\mathrm{C}_{\mathrm{1}} \\ $$$${y}\:=\:\pm\sqrt{\mathrm{ln}\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\mid+\mathrm{C}_{\mathrm{2}} } \\ $$
Answered by ZaidMNuri last updated on 01/Jan/21
![dx=(x^2 −1)ydy (dx/((x^2 −1)))=ydy ∫(dx/((x^2 −1)))=∫ydy (1/2)∫[(1/(x−1))−(1/(x+1))]dx=(y^2 /2)+C (1/2)ln∣((x−1)/(x+1))∣=(y^2 /2)+C y=∓(√(ln∣((x−1)/(x+1))∣−2C))](https://www.tinkutara.com/question/Q127767.png)
$${dx}=\left({x}^{\mathrm{2}} −\mathrm{1}\right){ydy} \\ $$$$\frac{{dx}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)}={ydy} \\ $$$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)}=\int{ydy} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\left[\frac{\mathrm{1}}{{x}−\mathrm{1}}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right]{dx}=\frac{{y}^{\mathrm{2}} }{\mathrm{2}}+{C} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\mid=\frac{{y}^{\mathrm{2}} }{\mathrm{2}}+{C} \\ $$$${y}=\mp\sqrt{{ln}\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\mid−\mathrm{2}{C}} \\ $$
