Question Number 32688 by Rio Mike last updated on 31/Mar/18
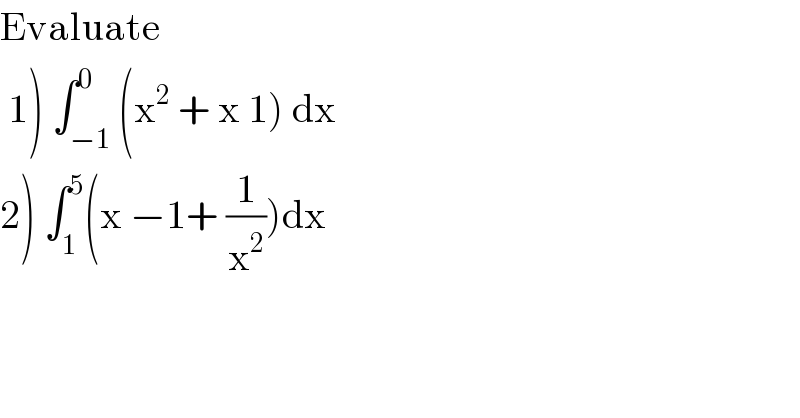
$$\mathrm{Evaluate} \\ $$$$\left.\:\mathrm{1}\right)\:\int_{−\mathrm{1}} ^{\mathrm{0}} \left(\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{x}\:\mathrm{1}\right)\:\mathrm{dx} \\ $$$$\left.\mathrm{2}\right)\:\int_{\mathrm{1}} ^{\mathrm{5}} \left(\mathrm{x}\:−\mathrm{1}+\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx} \\ $$$$ \\ $$
Answered by Joel578 last updated on 31/Mar/18
![(1) I = ∫_(−1) ^0 x^2 + x + 1 dx = [(1/3)x^3 + (1/2)x^2 + x]_(−1) ^0 = (0) − (−(1/3) + (1/2) − 1) = ... (2) I = ∫_1 ^5 x − 1 + (1/x^2 ) dx = [(1/2)x^2 − x − (1/x)]_1 ^5 = (((25)/2) − 5 − (1/5)) − ((1/2) − 1 − 1) = ...](https://www.tinkutara.com/question/Q32697.png)
$$\left(\mathrm{1}\right) \\ $$$${I}\:=\:\int_{−\mathrm{1}} ^{\mathrm{0}} \:{x}^{\mathrm{2}} \:+\:{x}\:+\:\mathrm{1}\:{dx} \\ $$$$\:\:\:=\:\left[\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} \:+\:\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \:+\:{x}\right]_{−\mathrm{1}} ^{\mathrm{0}} \\ $$$$\:\:\:=\:\left(\mathrm{0}\right)\:−\:\left(−\frac{\mathrm{1}}{\mathrm{3}}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:−\:\mathrm{1}\right) \\ $$$$\:\:\:=\:… \\ $$$$ \\ $$$$\left(\mathrm{2}\right) \\ $$$${I}\:=\:\int_{\mathrm{1}} ^{\mathrm{5}} \:{x}\:−\:\mathrm{1}\:+\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:{dx} \\ $$$$\:\:\:=\:\left[\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \:−\:{x}\:−\:\frac{\mathrm{1}}{{x}}\right]_{\mathrm{1}} ^{\mathrm{5}} \\ $$$$\:\:\:=\:\left(\frac{\mathrm{25}}{\mathrm{2}}\:−\:\mathrm{5}\:−\:\frac{\mathrm{1}}{\mathrm{5}}\right)\:−\:\left(\frac{\mathrm{1}}{\mathrm{2}}\:−\:\mathrm{1}\:−\:\mathrm{1}\right) \\ $$$$\:\:\:=\:… \\ $$
