Question Number 81482 by Bash last updated on 13/Feb/20
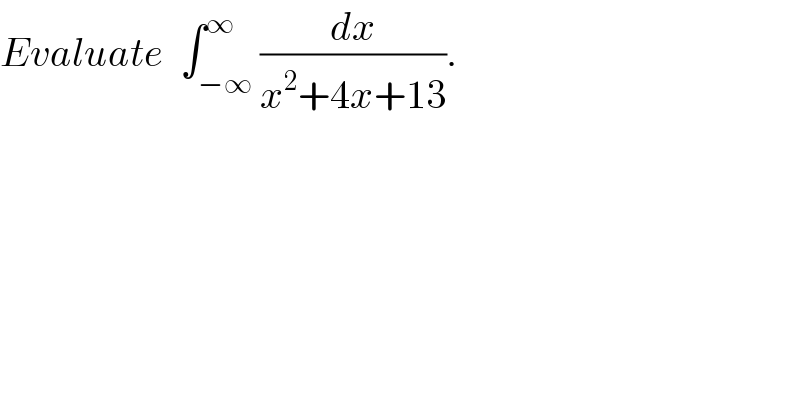
$${Evaluate}\:\:\int_{−\infty} ^{\infty} \frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{13}}. \\ $$
Commented by abdomathmax last updated on 13/Feb/20
![I=∫_(−∞) ^(+∞) (dx/(x^2 +4x +13)) =∫_(−∞) ^(+∞) (dx/(x^2 +4x+4+9)) =∫_(−∞) ^(+∞) (dx/((x+2)^2 +9)) =_(x+2=3u) ∫_(−∞) ^(+∞) ((3du)/(9(u^2 +1))) =(1/3) ∫_(−∞) ^(+∞) (du/(u^2 +1))=(1/3)[arctanu]_(−∞) ^(+∞) =(1/3)((π/2)−(−(π/2))) =(π/3)](https://www.tinkutara.com/question/Q81503.png)
$${I}=\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{4}{x}\:+\mathrm{13}}\:=\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}+\mathrm{9}} \\ $$$$=\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\left({x}+\mathrm{2}\right)^{\mathrm{2}} \:+\mathrm{9}}\:=_{{x}+\mathrm{2}=\mathrm{3}{u}} \:\:\int_{−\infty} ^{+\infty} \frac{\mathrm{3}{du}}{\mathrm{9}\left({u}^{\mathrm{2}} +\mathrm{1}\right)}\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\:\int_{−\infty} ^{+\infty} \:\frac{{du}}{{u}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{3}}\left[{arctanu}\right]_{−\infty} ^{+\infty} =\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\pi}{\mathrm{2}}−\left(−\frac{\pi}{\mathrm{2}}\right)\right) \\ $$$$=\frac{\pi}{\mathrm{3}} \\ $$
Answered by MJS last updated on 13/Feb/20
![∫(dx/(x^2 +4x+13))= [t=((x+2)/3) → dx=3dt] =(1/3)∫(dt/(t^2 +1))=(1/3)arctan t =(1/3)arctan ((x+2)/3) +C ∫_(−∞) ^(+∞) (dx/(x^2 +4x+13))=(π/3)](https://www.tinkutara.com/question/Q81487.png)
$$\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{13}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{{x}+\mathrm{2}}{\mathrm{3}}\:\rightarrow\:{dx}=\mathrm{3}{dt}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arctan}\:{t}\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arctan}\:\frac{{x}+\mathrm{2}}{\mathrm{3}}\:+{C} \\ $$$$\underset{−\infty} {\overset{+\infty} {\int}}\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{13}}=\frac{\pi}{\mathrm{3}} \\ $$
