Question Number 175409 by henderson last updated on 29/Aug/22
$$\mathrm{exercise} \\ $$Consider a polygon with an odd number π» of vertices. We connect any 3 vertices of this polygon to form a triangle.
What is the probability that this triangle contains the center of the circle circumscribing the polygon?
Commented by nikif99 last updated on 01/Sep/22
$${I}\:{think}\:{there}\:{is}\:{no}\:{solution}\:{for}\:{non} \\ $$$${regular}\:{polygons}. \\ $$
Commented by greg_ed last updated on 31/Aug/22
$$\boldsymbol{\mathrm{no}}\:\boldsymbol{\mathrm{idea}}\:! \\ $$
Commented by mr W last updated on 04/Sep/22
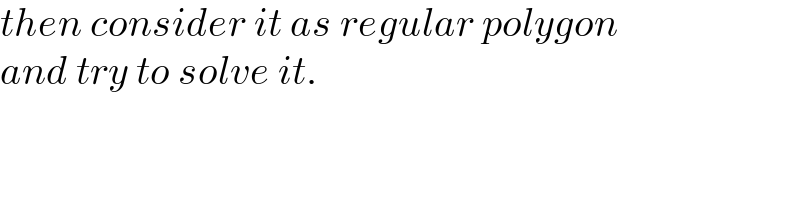
$${then}\:{consider}\:{it}\:{as}\:{regular}\:{polygon} \\ $$$${and}\:{try}\:{to}\:{solve}\:{it}. \\ $$
Commented by nikif99 last updated on 04/Jan/26
$$\bullet\:{Results}\:{are}\:{checked}\:{via}\:{Python}\:{and} \\ $$$${Fortran}\:{developed}\:{software}. \\ $$$${An}\:{indicative}\:{output}\:{is}\:{here}. \\ $$$$\bullet\:{As}\:{n}\:{increases},\:{probability}\:{trends} \\ $$$${to}\:\mathrm{0}.\mathrm{25} \\ $$
Commented by nikif99 last updated on 04/Jan/26
Answered by nikif99 last updated on 04/Jan/26
![This is obtained after a communication to a math forum (quora.com) and the valuable help and solution of Steven Smith. β’ a, b, c are the sides of a reg. n-gon with aβ€bβ€c β’ Their length does not exceed d=βn/2β β’ Schema is named a set of triples {a, b, c} indifferently of their order, summing up n. Each schema is repeated kΓn cases {kβN} except for equilateral triangles where only n/3 cases occur. (for a 9-gon 3 schemas exist: {1,4,4} (1Γ9 cases, k=1), {2,3,4} (2Γ9 cases), {3,3,3} (9/3 cases) Using stars and bars and inclusion-exclusion principle, the number of 3-tuples (not combinations) is calculated S=Ξ£_(i=0) ^2 [(β1)^i ((3),(i) ) (((nβiΓdβ1)),(( 2)) )] (1) Then to change into permutations, we need to substract how many of those have at least 2 identical elements 3β((nβ2Γβ((nβd)/2)β+1)/2)ββ2(n%3==0) The term 2(n%3==0) expresses the reduction by 2 when n is a multiple of 3, i.e an equilateral triangle is formed with a=b=c. After subtracting, we get the number of permutations, and then to change into combinations we divide by (3!) to reach the number of combinations B. This is the numver of schemas for a given n-gon. B=((SΒ±3β((nβ2Γβ((nβd)/2)β+1)/2)β+2(n%3==0))/6) (2) Remarks for (2) -When calculating ((p),(q) ) becomes unattainable (i.e p<1 or p<q) the result is set to 0. -Signing the 2nd term of the numerator by (+) you allow tuples with repeated elements, like {5,5,7}, (in other words is the number of schemas), while by (β) not. {Another formula to obtain tbe number of schemas is Ξ£_(i=βn/3β) ^(βn/2β) (iββ((nβi)/2)β+1) } In the preceding formula (2) we omit the 2nd term of the numerator, then multiplying by 2 the sum of k factors is obtained. K=((S+2(n%3==0))/3) Therefore, the number of requested triangles could be A=Kβn In the case of equilateral triangle, a full value of k is counted, so we reduce by 2n/3. A=Kβnβ((2n)/3)(n%3==0) Therefore, the number of triangles enclosing the circumcenter is A=((S+2(n%3==0))/3)βnβ((2n)/3)(n%3==0) which after simplification and restoring S from (1) turns into A=((Ξ£_(i=0) ^2 [(β1)^i ((3),(i) ) (((nβiΓdβ1)),(( 2)) )])/3)βn Finally, the demanded probability is determinant (((P=((Ξ£_(i=0) ^2 [(β1)^i ((3),(i) ) (((nβiΓdβ1)),(( 2)) )]n)/(3 ((n),(3) ))))))](https://www.tinkutara.com/question/Q227175.png)
$${This}\:{is}\:{obtained}\:{after}\:{a}\:{communication}\:{to}\:{a} \\ $$$${math}\:{forum}\:\left({quora}.{com}\right)\:{and}\:{the}\:{valuable} \\ $$$${help}\:{and}\:{solution}\:{of}\:{Steven}\:{Smith}. \\ $$$$\bullet\:{a},\:{b},\:{c}\:{are}\:{the}\:{sides}\:{of}\:{a}\:{reg}.\:{n}-{gon}\:{with}\:{a}\leqslant{b}\leqslant{c} \\ $$$$\bullet\:{Their}\:{length}\:{does}\:{not}\:{exceed}\:{d}=\lfloor{n}/\mathrm{2}\rfloor \\ $$$$\bullet\:{Schema}\:{is}\:{named}\:{a}\:{set}\:{of}\:{triples}\:\left\{{a},\:{b},\:{c}\right\} \\ $$$${indifferently}\:{of}\:{their}\:{order},\:{summing}\:{up}\:{n}. \\ $$$${Each}\:{schema}\:{is}\:{repeated}\:{k}Γ{n}\:{cases}\:\left\{{k}\in\mathbb{N}\right\} \\ $$$${except}\:{for}\:{equilateral}\:{triangles}\:{where}\:{only} \\ $$$${n}/\mathrm{3}\:{cases}\:{occur}. \\ $$$$\left({for}\:{a}\:\mathrm{9}-{gon}\:\mathrm{3}\:{schemas}\:{exist}:\:\left\{\mathrm{1},\mathrm{4},\mathrm{4}\right\}\:\left(\mathrm{1}Γ\mathrm{9}\right.\right. \\ $$$$\left.{cases},\:{k}=\mathrm{1}\right),\:\left\{\mathrm{2},\mathrm{3},\mathrm{4}\right\}\:\left(\mathrm{2}Γ\mathrm{9}\:{cases}\right),\:\left\{\mathrm{3},\mathrm{3},\mathrm{3}\right\}\:\left(\mathrm{9}/\mathrm{3}\:{cases}\right) \\ $$$$\boldsymbol{{Using}}\:{stars}\:{and}\:{bars}\:{and}\:{inclusion}-{exclusion} \\ $$$${principle},\:{the}\:{number}\:{of}\:\mathrm{3}-{tuples}\:\left({not}\right. \\ $$$$\left.{combinations}\right)\:{is}\:{calculated} \\ $$$${S}=\underset{{i}=\mathrm{0}} {\overset{\mathrm{2}} {\sum}}\left[\left(β\mathrm{1}\right)^{{i}} \begin{pmatrix}{\mathrm{3}}\\{{i}}\end{pmatrix}\begin{pmatrix}{{n}β{i}Γ{d}β\mathrm{1}}\\{\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}}\end{pmatrix}\right]\:\left(\mathrm{1}\right) \\ $$$${Then}\:{to}\:{change}\:{into}\:{permutations},\:{we}\:{need}\:{to} \\ $$$${substract}\:{how}\:{many}\:{of}\:{those}\:{have}\:{at}\:{least} \\ $$$$\mathrm{2}\:{identical}\:{elements} \\ $$$$\mathrm{3}\lfloor\frac{{n}β\mathrm{2}Γ\lceil\frac{{n}β{d}}{\mathrm{2}}\rceil+\mathrm{1}}{\mathrm{2}}\rfloorβ\mathrm{2}\left({n\%}\mathrm{3}==\mathrm{0}\right) \\ $$$${The}\:{term}\:\mathrm{2}\left({n\%}\mathrm{3}==\mathrm{0}\right)\:{expresses}\:{the}\:{reduction} \\ $$$${by}\:\mathrm{2}\:{when}\:{n}\:{is}\:{a}\:{multiple}\:{of}\:\mathrm{3},\:{i}.{e}\:{an}\:{equilateral} \\ $$$${triangle}\:{is}\:{formed}\:{with}\:{a}={b}={c}. \\ $$$${After}\:{subtracting},\:{we}\:{get}\:{the}\:{number}\:{of} \\ $$$${permutations},\:{and}\:{then}\:{to}\:{change}\:{into} \\ $$$${combinations}\:{we}\:{divide}\:{by}\:\left(\mathrm{3}!\right)\:{to}\:{reach}\:{the} \\ $$$${number}\:{of}\:{combinations}\:{B}.\:{This}\:{is}\:{the}\:{numver} \\ $$$${of}\:{schemas}\:{for}\:{a}\:{given}\:{n}-{gon}. \\ $$$${B}=\frac{{S}\pm\mathrm{3}\lfloor\frac{{n}β\mathrm{2}Γ\lceil\frac{{n}β{d}}{\mathrm{2}}\rceil+\mathrm{1}}{\mathrm{2}}\rfloor+\mathrm{2}\left({n\%}\mathrm{3}==\mathrm{0}\right)}{\mathrm{6}}\:\left(\mathrm{2}\right) \\ $$$${Remarks}\:{for}\:\left(\mathrm{2}\right) \\ $$$$-{When}\:{calculating}\:\begin{pmatrix}{{p}}\\{{q}}\end{pmatrix}\:{becomes}\:{unattainable} \\ $$$$\left({i}.{e}\:{p}<\mathrm{1}\:{or}\:{p}<{q}\right)\:{the}\:{result}\:{is}\:{set}\:{to}\:\mathrm{0}. \\ $$$$-{Signing}\:{the}\:\mathrm{2}{nd}\:{term}\:{of}\:{the}\:{numerator}\:{by}\:\left(+\right) \\ $$$${you}\:{allow}\:{tuples}\:{with}\:{repeated}\:{elements},\:{like} \\ $$$$\left\{\mathrm{5},\mathrm{5},\mathrm{7}\right\},\:\left({in}\:{other}\:{words}\:{is}\:{the}\:{number}\:{of}\right. \\ $$$$\left.{schemas}\right),\:{while}\:{by}\:\left(β\right)\:{not}. \\ $$$$\left\{{Another}\:{formula}\:{to}\:{obtain}\:{tbe}\:{number}\:{of}\right. \\ $$$${schemas}\:{is} \\ $$$$\underset{{i}=\lceil{n}/\mathrm{3}\rceil} {\overset{\lfloor{n}/\mathrm{2}\rfloor} {\sum}}\left({i}β\lceil\frac{{n}β{i}}{\mathrm{2}}\rceil+\mathrm{1}\right) \\ $$$$\left.\right\} \\ $$$${In}\:{the}\:{preceding}\:{formula}\:\left(\mathrm{2}\right)\:{we}\:{omit}\:{the}\:\mathrm{2}{nd} \\ $$$${term}\:{of}\:{the}\:{numerator},\:{then}\:{multiplying}\:{by}\:\mathrm{2} \\ $$$${the}\:{sum}\:{of}\:{k}\:{factors}\:{is}\:{obtained}. \\ $$$${K}=\frac{{S}+\mathrm{2}\left({n\%}\mathrm{3}==\mathrm{0}\right)}{\mathrm{3}} \\ $$$${Therefore},\:{the}\:{number}\:{of}\:{requested}\:{triangles} \\ $$$${could}\:{be} \\ $$$${A}={K}\centerdot{n} \\ $$$${In}\:{the}\:{case}\:{of}\:{equilateral}\:{triangle},\:{a}\:{full}\:{value} \\ $$$${of}\:{k}\:{is}\:{counted},\:{so}\:{we}\:{reduce}\:{by}\:\mathrm{2}{n}/\mathrm{3}. \\ $$$${A}={K}\centerdot{n}β\frac{\mathrm{2}{n}}{\mathrm{3}}\left({n\%}\mathrm{3}==\mathrm{0}\right) \\ $$$${Therefore},\:{the}\:{number}\:{of}\:{triangles}\:{enclosing} \\ $$$${the}\:{circumcenter}\:{is} \\ $$$${A}=\frac{{S}+\cancel{\mathrm{2}\left({n\%}\mathrm{3}==\mathrm{0}\right)}}{\mathrm{3}}\centerdot{n}β\cancel{\frac{\mathrm{2}{n}}{\mathrm{3}}\left({n\%}\mathrm{3}==\mathrm{0}\right)} \\ $$$${which}\:{after}\:{simplification}\:{and}\:{restoring}\:{S} \\ $$$${from}\:\left(\mathrm{1}\right)\:{turns}\:{into} \\ $$$${A}=\frac{\underset{{i}=\mathrm{0}} {\overset{\mathrm{2}} {\sum}}\left[\left(β\mathrm{1}\right)^{{i}} \begin{pmatrix}{\mathrm{3}}\\{{i}}\end{pmatrix}\begin{pmatrix}{{n}β{i}Γ{d}β\mathrm{1}}\\{\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}}\end{pmatrix}\right]}{\mathrm{3}}\centerdot{n} \\ $$$${Finally},\:{the}\:{demanded}\:{probability}\:{is} \\ $$$$\begin{array}{|c|}{{P}=\frac{\underset{{i}=\mathrm{0}} {\overset{\mathrm{2}} {\sum}}\left[\left(β\mathrm{1}\right)^{{i}} \begin{pmatrix}{\mathrm{3}}\\{{i}}\end{pmatrix}\begin{pmatrix}{{n}β{i}Γ{d}β\mathrm{1}}\\{\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}}\end{pmatrix}\right]{n}}{\mathrm{3}\begin{pmatrix}{{n}}\\{\mathrm{3}}\end{pmatrix}}}\\\hline\end{array} \\ $$