Question Number 147275 by ArielVyny last updated on 19/Jul/21
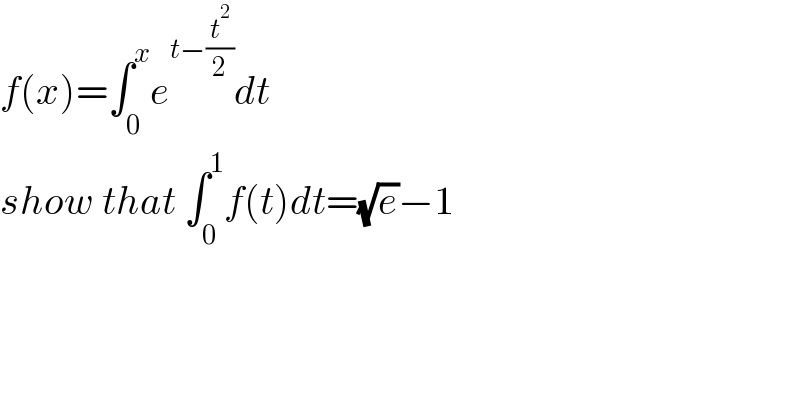
$${f}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} {e}^{{t}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} {dt}\: \\ $$$${show}\:{that}\:\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({t}\right){dt}=\sqrt{{e}}−\mathrm{1} \\ $$
Answered by mindispower last updated on 19/Jul/21
![∫_0 ^1 f(t)dt=[tf(t)]_0 ^1 −∫_0 ^1 tf′(t)dt =f(1)−∫_0 ^1 te^(t−(t^2 /2)) dt =∫_0 ^1 (1−t)e^(t−(t^2 /2)) dt=[e^(t−(t^2 /2)) ]_0 ^1 =(√e)−1](https://www.tinkutara.com/question/Q147318.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({t}\right){dt}=\left[{tf}\left({t}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} {tf}'\left({t}\right){dt} \\ $$$$={f}\left(\mathrm{1}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} {te}^{{t}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} {dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{t}\right){e}^{{t}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} {dt}=\left[{e}^{{t}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} \right]_{\mathrm{0}} ^{\mathrm{1}} =\sqrt{{e}}−\mathrm{1} \\ $$
Commented by ArielVyny last updated on 20/Jul/21

$${thank}\:{sir} \\ $$
