Question Number 105593 by Study last updated on 30/Jul/20
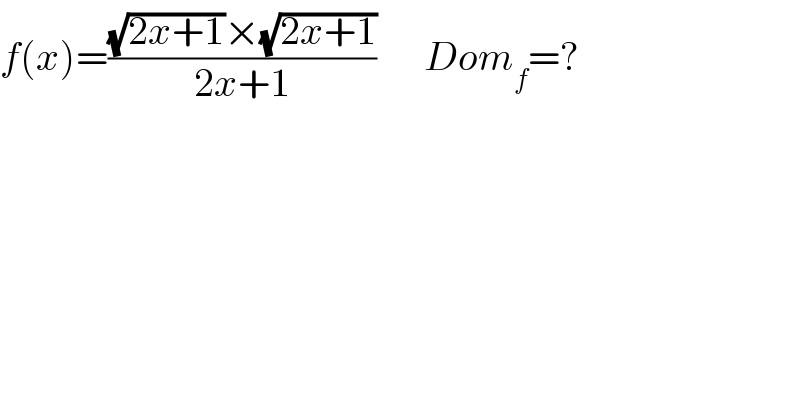
$${f}\left({x}\right)=\frac{\sqrt{\mathrm{2}{x}+\mathrm{1}}×\sqrt{\mathrm{2}{x}+\mathrm{1}}}{\mathrm{2}{x}+\mathrm{1}}\:\:\:\:\:\:{Dom}_{{f}} =? \\ $$
Answered by mathmax by abdo last updated on 30/Jul/20
![D_f =]−(1/2),+∞[](https://www.tinkutara.com/question/Q105618.png)
$$\left.\mathrm{D}_{\mathrm{f}} =\right]−\frac{\mathrm{1}}{\mathrm{2}},+\infty\left[\right. \\ $$
Commented by Study last updated on 30/Jul/20
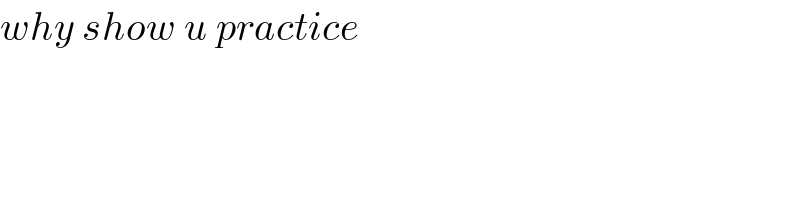
$${why}\:{show}\:{u}\:{practice} \\ $$
Answered by mathmax by abdo last updated on 30/Jul/20
![what practice here ? x∈ Df ⇔ 2x+1 ≥0 and 2x+1 ≠0 ⇒2x+1>0 ⇒ x>−(1/2) ⇒D_f =]−(1/2),+∞[](https://www.tinkutara.com/question/Q105669.png)
$$\mathrm{what}\:\mathrm{practice}\:\mathrm{here}\:?\:\:\:\mathrm{x}\in\:\mathrm{Df}\:\Leftrightarrow\:\mathrm{2x}+\mathrm{1}\:\geqslant\mathrm{0}\:\mathrm{and}\:\mathrm{2x}+\mathrm{1}\:\neq\mathrm{0}\:\Rightarrow\mathrm{2x}+\mathrm{1}>\mathrm{0}\:\Rightarrow \\ $$$$\left.\mathrm{x}>−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{D}_{\mathrm{f}} =\right]−\frac{\mathrm{1}}{\mathrm{2}},+\infty\left[\right. \\ $$
