Question Number 35429 by abdo.msup.com last updated on 18/May/18
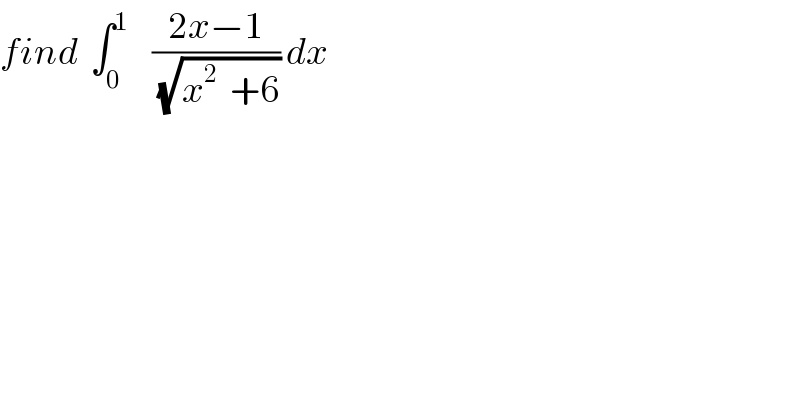
$${find}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} \:\:+\mathrm{6}}}\:{dx} \\ $$
Commented by prof Abdo imad last updated on 19/May/18
![let put I = ∫_0 ^1 ((2x−1)/( (√(x^2 +6)))) .changement x=(√6)sht give I = ∫_0 ^(argsh((1/( (√6))))) ((2(√6) sht −1)/( (√6)ch(t))) (√6) cht dt = ∫_0 ^(ln( (1/( (√6))) +(√(1+(1/6)))) (2(√6) sh(t)−1)dt =2(√6) [ ch(t)]_0 ^(ln( (1/( (√6))) +(√(7/6)))) −ln((1/( (√6))) +((√7)/( (√6)))) we have ch(t) =((e^t +e^(−t) )/2) ⇒ ch{ ln( (1/( (√6))) +((√7)/( (√6))))} = ((((1/( (√6))) +((√7)/( (√6)))) +((1/( (√6)))+((√7)/( (√6))))^(−1) )/2) ⇒ I = 2(√6){ ((((1/( (√6)))+((√7)/( (√6)))) +((1/( (√6))) +((√7)/( (√6))))^(−1) )/2) −1} −ln((1/( (√6))) +((√7)/( (√6))))](https://www.tinkutara.com/question/Q35449.png)
$${let}\:{put}\:{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{6}}}\:.{changement}\:{x}=\sqrt{\mathrm{6}}{sht} \\ $$$${give}\:{I}\:=\:\int_{\mathrm{0}} ^{{argsh}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}\right)} \:\:\:\:\:\frac{\mathrm{2}\sqrt{\mathrm{6}}\:{sht}\:−\mathrm{1}}{\:\sqrt{\mathrm{6}}{ch}\left({t}\right)}\:\sqrt{\mathrm{6}}\:{cht}\:{dt} \\ $$$$=\:\int_{\mathrm{0}} ^{{ln}\left(\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}\:+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{6}}}\right.} \:\left(\mathrm{2}\sqrt{\mathrm{6}}\:{sh}\left({t}\right)−\mathrm{1}\right){dt} \\ $$$$=\mathrm{2}\sqrt{\mathrm{6}}\:\left[\:{ch}\left({t}\right)\right]_{\mathrm{0}} ^{{ln}\left(\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}\:+\sqrt{\frac{\mathrm{7}}{\mathrm{6}}}\right)} \:−{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}\:+\frac{\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{6}}}\right) \\ $$$${we}\:{have}\:{ch}\left({t}\right)\:=\frac{{e}^{{t}} \:+{e}^{−{t}} }{\mathrm{2}}\:\Rightarrow\: \\ $$$${ch}\left\{\:{ln}\left(\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}\:+\frac{\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{6}}}\right)\right\}\:=\:\frac{\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}\:+\frac{\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{6}}}\right)\:+\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}+\frac{\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{6}}}\right)^{−\mathrm{1}} }{\mathrm{2}}\:\Rightarrow \\ $$$${I}\:=\:\mathrm{2}\sqrt{\mathrm{6}}\left\{\:\:\frac{\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}+\frac{\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{6}}}\right)\:+\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}\:+\frac{\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{6}}}\right)^{−\mathrm{1}} }{\mathrm{2}}\:−\mathrm{1}\right\} \\ $$$$−{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}\:+\frac{\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{6}}}\right) \\ $$
Answered by ajfour last updated on 19/May/18

$${I}=\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{\mathrm{2}{xdx}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{6}}}−\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} +\left(\sqrt{\mathrm{6}}\right)^{\mathrm{2}} }} \\ $$$$\:\:=\mathrm{2}\sqrt{{x}^{\mathrm{2}} +\mathrm{6}}\mid_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{ln}\:\mid{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{6}}\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\Rightarrow\:{I}=\mathrm{2}\left(\sqrt{\mathrm{7}}−\sqrt{\mathrm{6}}\right)−\mathrm{ln}\:\left(\frac{\mathrm{1}+\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{6}}}\right) \\ $$
