Question Number 123676 by mathmax by abdo last updated on 27/Nov/20
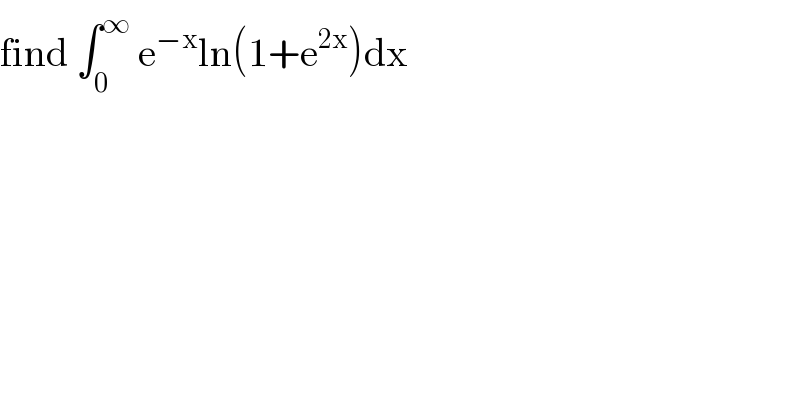
$$\mathrm{find}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{\mathrm{2x}} \right)\mathrm{dx} \\ $$
Answered by mnjuly1970 last updated on 27/Nov/20
![solution Ω=∫_0 ^( ∞) e^(−x) ln[e^(2x) (1+e^(−2x) )]dx =2∫_0 ^( ∞) xe^(−x) dx+∫_0 ^( ∞) e^(−x) ln(1+e^(−2x) )dx =2Γ(2)+∫_0 ^( ∞) e^(−x) Σ_(n=1 ) ^∞ (((−1)^(n−1) e^(−2nx) )/n)dx =2+Σ_(n=1) ^∞ (((−1)^(n−1) )/n)∫_0 ^( ∞) e^(−x(2n+1)) dx =2+Σ_(n=1) ^∞ (((−1)^n )/n)[(e^(−x(2n+1)) /(2n+1))]_0 ^∞ =2+Σ_(n=1 ) ^∞ (((−1)^(n−1) )/(n(2n+1)))=2−[Σ_(n=1 ) ^∞ (((−1)^n )/n)−((2(−1)^n )/(2n+1))] =2+ln(2)+2[−1+(π/4)] ln(2)+(π/2) ≈2.26](https://www.tinkutara.com/question/Q123682.png)
$${solution} \\ $$$$\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\infty} {e}^{−{x}} {ln}\left[{e}^{\mathrm{2}{x}} \left(\mathrm{1}+{e}^{−\mathrm{2}{x}} \right)\right]{dx} \\ $$$$\:\:\:=\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} {xe}^{−{x}} {dx}+\int_{\mathrm{0}} ^{\:\infty} {e}^{−{x}} {ln}\left(\mathrm{1}+{e}^{−\mathrm{2}{x}} \right){dx} \\ $$$$=\mathrm{2}\Gamma\left(\mathrm{2}\right)+\int_{\mathrm{0}} ^{\:\infty} {e}^{−{x}} \underset{{n}=\mathrm{1}\:} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {e}^{−\mathrm{2}{nx}} }{{n}}{dx} \\ $$$$=\mathrm{2}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\int_{\mathrm{0}} ^{\:\infty} {e}^{−{x}\left(\mathrm{2}{n}+\mathrm{1}\right)} {dx} \\ $$$$=\mathrm{2}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\left[\frac{{e}^{−{x}\left(\mathrm{2}{n}+\mathrm{1}\right)} }{\mathrm{2}{n}+\mathrm{1}}\right]_{\mathrm{0}} ^{\infty} \\ $$$$=\mathrm{2}+\underset{{n}=\mathrm{1}\:} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}\left(\mathrm{2}{n}+\mathrm{1}\right)}=\mathrm{2}−\left[\underset{{n}=\mathrm{1}\:} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}−\frac{\mathrm{2}\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\right] \\ $$$$\:=\mathrm{2}+{ln}\left(\mathrm{2}\right)+\mathrm{2}\left[−\mathrm{1}+\frac{\pi}{\mathrm{4}}\right] \\ $$$$\:\:{ln}\left(\mathrm{2}\right)+\frac{\pi}{\mathrm{2}}\:\approx\mathrm{2}.\mathrm{26} \\ $$
Commented by mnjuly1970 last updated on 27/Nov/20

Commented by harckinwunmy last updated on 27/Nov/20
$$\mathrm{can}\:\mathrm{i}\:\mathrm{know}\:\mathrm{the}\:\mathrm{name}\:\mathrm{og}\: \\ $$$$\mathrm{this}\:\mathrm{app}.\:\mathrm{thanks} \\ $$
Commented by Dwaipayan Shikari last updated on 27/Nov/20

$${Wolfram}\:{alpha} \\ $$
Commented by Dwaipayan Shikari last updated on 27/Nov/20
https://wolframalpha.com/
Commented by mnjuly1970 last updated on 27/Nov/20

$$\:{thank}\:{you}\:{mr}\:{payan} \\ $$
Commented by Dwaipayan Shikari last updated on 27/Nov/20
��
Commented by mathmax by abdo last updated on 28/Nov/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{mn}… \\ $$
Answered by mathmax by abdo last updated on 28/Nov/20
![I=∫_0 ^∞ e^(−x) ln(1+e^(2x) )dx changement e^x =t give I =∫_1 ^∞ t^(−1) ln(1+t^2 )(dt/t) =∫_1 ^∞ ((ln(1+t^2 ))/t^2 )dt =_(bypsrts) [−(1/t)ln(1+t^2 )]_1 ^∞ +∫_1 ^∞ (1/t)×((2t)/(1+t^2 ))dt =ln(2) +2∫_1 ^∞ (dt/(1+t^2 )) =ln(2)+2[arctant]_1 ^∞ =ln(2)+2{(π/2)−(π/4)} =ln(2)+2((π/4)) =(π/2) +ln(2)](https://www.tinkutara.com/question/Q123757.png)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{\mathrm{2x}} \right)\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{e}^{\mathrm{x}} \:=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{I}\:=\int_{\mathrm{1}} ^{\infty} \:\mathrm{t}^{−\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\frac{\mathrm{dt}}{\mathrm{t}}\:=\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\: \\ $$$$=_{\mathrm{bypsrts}} \:\:\:\left[−\frac{\mathrm{1}}{\mathrm{t}}\mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\right]_{\mathrm{1}} ^{\infty} +\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{\mathrm{t}}×\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\mathrm{ln}\left(\mathrm{2}\right)\:+\mathrm{2}\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:=\mathrm{ln}\left(\mathrm{2}\right)+\mathrm{2}\left[\mathrm{arctant}\right]_{\mathrm{1}} ^{\infty} \\ $$$$=\mathrm{ln}\left(\mathrm{2}\right)+\mathrm{2}\left\{\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\right\}\:=\mathrm{ln}\left(\mathrm{2}\right)+\mathrm{2}\left(\frac{\pi}{\mathrm{4}}\right)\:=\frac{\pi}{\mathrm{2}}\:+\mathrm{ln}\left(\mathrm{2}\right) \\ $$
