Question Number 28811 by abdo imad last updated on 30/Jan/18
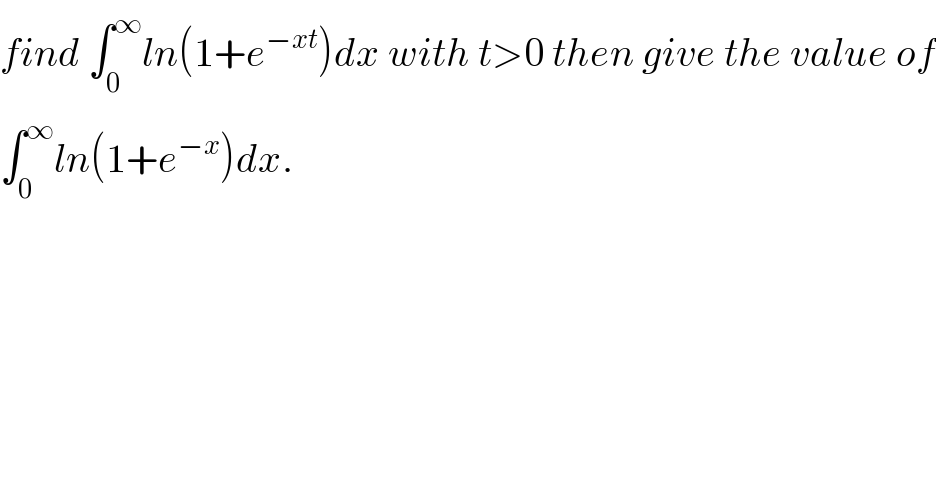
$${find}\:\int_{\mathrm{0}} ^{\infty} {ln}\left(\mathrm{1}+{e}^{−{xt}} \right){dx}\:{with}\:{t}>\mathrm{0}\:{then}\:{give}\:{the}\:{value}\:{of} \\ $$$$\int_{\mathrm{0}} ^{\infty} {ln}\left(\mathrm{1}+{e}^{−{x}} \right){dx}. \\ $$
Commented by abdo imad last updated on 01/Feb/18
![we havefor ∣u∣<1 (d/du)(ln(1+u))= (1/(1+u))= Σ_(n=0) ^∞ (−1)^n u^n ⇒ ln(1+u)= Σ_(n=0) ^∞ (((−1)^n )/(n+1))u^(n+1 ) +k (k=ln(1)=0) so ln(1+u)= Σ_(n=1) ^∞ (((−1)^(n−1) )/n) u^n and ∫_0 ^∞ ln(1+ e^(−xt) )dx =∫_0 ^∞ (Σ_(n=1) ^∞ (((−1)^(n−1) )/n) e^(−nxt) )dx = Σ_(n=1) ^∞ (((−1)^(n−1) )/n) ∫_0 ^∞ e^(−ntx) dx= Σ_(n=1) ^∞ (((−1)^(n−1) )/n) A_n A_n = ∫_0 ^∞ e^(−ntx) dx = ((−1)/(nt)) [ e^(−ntx) ]_(x=0) ^∞ = (1/(nt)) so ∫_0 ^∞ ln(1+ e^(−xt) )dx= (1/t) Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 )=−(1/t)δ(2) δ(x)= Σ_(n=1) ^∞ (((−1)^n )/n^x ) we have proved that δ(x)=( 2^(1−x) −1)ξ(x) ⇒δ(2)= ((1/2) −1)ξ(2)=−(1/2) (π^2 /6) =−(π^2 /(12)) and ∫_0 ^∞ ln(1+ e^(−xt) )dx= (π^2 /(12t)) let take t=1 ∫_0 ^∞ ln(1+ e^(−x) )dx =(π^2 /(12)) .](https://www.tinkutara.com/question/Q28923.png)
$${we}\:{havefor}\:\mid{u}\mid<\mathrm{1}\:\:\frac{{d}}{{du}}\left({ln}\left(\mathrm{1}+{u}\right)\right)=\:\frac{\mathrm{1}}{\mathrm{1}+{u}}=\:\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {u}^{{n}} \:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{u}\right)=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}{u}^{{n}+\mathrm{1}\:} \:\:+{k}\:\:\:\:\:\:\:\left({k}={ln}\left(\mathrm{1}\right)=\mathrm{0}\right)\:{so} \\ $$$${ln}\left(\mathrm{1}+{u}\right)=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:{u}^{{n}} \:\:\:{and} \\ $$$$\int_{\mathrm{0}} ^{\infty} {ln}\left(\mathrm{1}+\:{e}^{−{xt}} \right){dx}\:=\int_{\mathrm{0}} ^{\infty} \left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:{e}^{−{nxt}} \right){dx} \\ $$$$=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{ntx}} {dx}=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\:{A}_{{n}} \\ $$$${A}_{{n}} =\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{ntx}} {dx}\:=\:\frac{−\mathrm{1}}{{nt}}\:\left[\:\:{e}^{−{ntx}} \right]_{{x}=\mathrm{0}} ^{\infty} =\:\frac{\mathrm{1}}{{nt}}\:{so} \\ $$$$\int_{\mathrm{0}} ^{\infty} {ln}\left(\mathrm{1}+\:{e}^{−{xt}} \right){dx}=\:\:\frac{\mathrm{1}}{{t}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} }=−\frac{\mathrm{1}}{{t}}\delta\left(\mathrm{2}\right) \\ $$$$\delta\left({x}\right)=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{{x}} }\:{we}\:{have}\:{proved}\:{that} \\ $$$$\delta\left({x}\right)=\left(\:\mathrm{2}^{\mathrm{1}−{x}} \:−\mathrm{1}\right)\xi\left({x}\right)\:\Rightarrow\delta\left(\mathrm{2}\right)=\:\left(\frac{\mathrm{1}}{\mathrm{2}}\:−\mathrm{1}\right)\xi\left(\mathrm{2}\right)=−\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$=−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:\:{and}\:\int_{\mathrm{0}} ^{\infty} {ln}\left(\mathrm{1}+\:{e}^{−{xt}} \right){dx}=\:\frac{\pi^{\mathrm{2}} }{\mathrm{12}{t}}\:\:\:{let}\:{take}\:{t}=\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{ln}\left(\mathrm{1}+\:{e}^{−{x}} \right){dx}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:. \\ $$$$ \\ $$
