Question Number 27502 by abdo imad last updated on 07/Jan/18
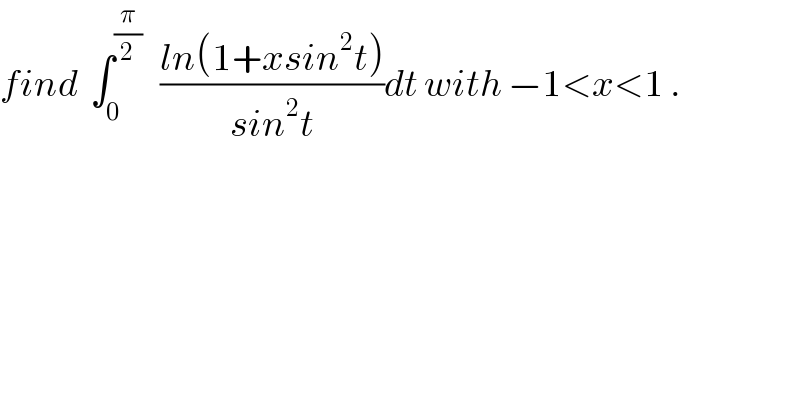
$${find}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{ln}\left(\mathrm{1}+{xsin}^{\mathrm{2}} {t}\right)}{{sin}^{\mathrm{2}} {t}}{dt}\:{with}\:−\mathrm{1}<{x}<\mathrm{1}\:. \\ $$
Commented by abdo imad last updated on 09/Jan/18
![let put f(x)= ∫_0 ^(π/2) ((ln(1+xsin^2 t))/(sin^2 t))dt after verifying that f is derivable on ]−1,1[ we have f^, (x)= ∫_0 ^(π/2) (dt/(1+xsin^2 t)) because of /xsin^2 t/<1 f^′ (x)= ∫_0 ^(π/2) ( Σ_(n=0) ^∝ (−1)^n x^n sin^(2n) t)dt =Σ_(n=0) ^∝ (−1)^n x^n ∫_0 ^(π/2) sin^(2n) tdt= Σ_(n=0) ^∝ (−1)^n W_n x^n with W_n = ∫_0 ^(π/2) sin^(2n) tdt and the value of W_n is known (walliss integral) f(x)= Σ_(n=0) ^∝ (((−1)^n )/(n+1)) W_n x^(n+1) +λ λ=f(0)=0⇒ f(x)= Σ_(n=0) ^∝ (((−1)^n )/(n+1)) W_n .x^(n+1) .](https://www.tinkutara.com/question/Q27573.png)
$${let}\:{put}\:{f}\left({x}\right)=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{ln}\left(\mathrm{1}+{xsin}^{\mathrm{2}} {t}\right)}{{sin}^{\mathrm{2}} {t}}{dt}\:{after}\:{verifying}\:{that}\:{f}\:{is} \\ $$$$\left.{derivable}\:{on}\:\right]−\mathrm{1},\mathrm{1}\left[\:{we}\:{have}\:{f}^{,} \left({x}\right)=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{dt}}{\mathrm{1}+{xsin}^{\mathrm{2}} {t}}\right. \\ $$$$\:{because}\:{of}\:/{xsin}^{\mathrm{2}} {t}/<\mathrm{1}\: \\ $$$${f}^{'} \left({x}\right)=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\:\sum_{{n}=\mathrm{0}} ^{\propto} \left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \:{sin}^{\mathrm{2}{n}} {t}\right){dt} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\propto} \left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}{n}} {tdt}=\:\sum_{{n}=\mathrm{0}} ^{\propto} \left(−\mathrm{1}\right)^{{n}} {W}_{{n}} \:{x}^{{n}} \\ $$$${with}\:{W}_{{n}} =\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}^{\mathrm{2}{n}} {tdt}\:\:{and}\:{the}\:{value}\:{of}\:{W}_{{n}} \:{is}\:{known} \\ $$$$\left({walliss}\:{integral}\right) \\ $$$${f}\left({x}\right)=\:\sum_{{n}=\mathrm{0}} ^{\propto} \frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}\:{W}_{{n}} \:{x}^{{n}+\mathrm{1}} \:\:\:+\lambda \\ $$$$\lambda={f}\left(\mathrm{0}\right)=\mathrm{0}\Rightarrow\:\:\:{f}\left({x}\right)=\:\sum_{{n}=\mathrm{0}} ^{\propto} \frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}\:{W}_{{n}} \:.{x}^{{n}+\mathrm{1}} \:\:\:. \\ $$$$ \\ $$
