Question Number 30761 by abdo imad last updated on 25/Feb/18
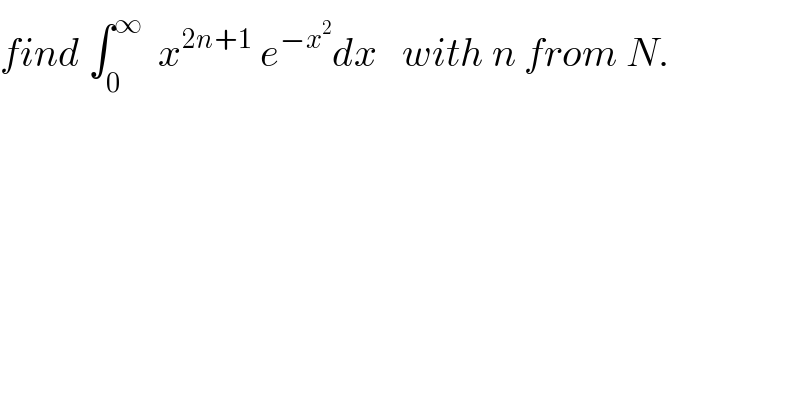
$${find}\:\int_{\mathrm{0}} ^{\infty} \:\:{x}^{\mathrm{2}{n}+\mathrm{1}} \:{e}^{−{x}^{\mathrm{2}} } {dx}\:\:\:{with}\:{n}\:{from}\:{N}. \\ $$
Commented by abdo imad last updated on 28/Feb/18
![let put A_n = ∫_0 ^∞ x^(2n+1) e^(−x^2 ) dx A_n = ((−1)/2) ∫_0 ^∞ x^(2n) (−2x e^(−x^2 ) )dx let ntegrate by parts u^′ =−2x e^(−x^2 ) and v=x^(2n) ⇒ A_n =−(1/2) ( [x^(2n) e^(−x^2 ) ]_0 ^∞ −∫_0 ^∞ 2n x^(2n−1) e^(−x^2 ) dx ) A_n =n A_(n−1) ⇒Π_(k=1) ^n A_k =n! Π_(k=1) ^n A_(k−1) ⇒ A_n =n! A_0 but A_0 = ∫_0 ^∞ x e^(−x^2 ) dx = [−(1/2)e^(−x^2 ) ]_0 ^∞ =(1/2) ⇒ A_n = ((n!)/2) .](https://www.tinkutara.com/question/Q30888.png)
$${let}\:{put}\:{A}_{{n}} =\:\int_{\mathrm{0}} ^{\infty} \:{x}^{\mathrm{2}{n}+\mathrm{1}} \:{e}^{−{x}^{\mathrm{2}} } {dx} \\ $$$${A}_{{n}} =\:\frac{−\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}{n}} \left(−\mathrm{2}{x}\:{e}^{−{x}^{\mathrm{2}} } \right){dx}\:{let}\:{ntegrate}\:{by}\:{parts} \\ $$$${u}^{'} =−\mathrm{2}{x}\:{e}^{−{x}^{\mathrm{2}} } \:{and}\:{v}={x}^{\mathrm{2}{n}} \:\Rightarrow \\ $$$${A}_{{n}} =−\frac{\mathrm{1}}{\mathrm{2}}\:\left(\:\:\left[{x}^{\mathrm{2}{n}} \:{e}^{−{x}^{\mathrm{2}} } \right]_{\mathrm{0}} ^{\infty} \:\:−\int_{\mathrm{0}} ^{\infty} \mathrm{2}{n}\:{x}^{\mathrm{2}{n}−\mathrm{1}} \:{e}^{−{x}^{\mathrm{2}} } \:{dx}\:\right) \\ $$$${A}_{{n}} ={n}\:{A}_{{n}−\mathrm{1}} \:\:\Rightarrow\prod_{{k}=\mathrm{1}} ^{{n}} \:{A}_{{k}} \:={n}!\:\prod_{{k}=\mathrm{1}} ^{{n}} \:{A}_{{k}−\mathrm{1}} \Rightarrow \\ $$$${A}_{{n}} ={n}!\:{A}_{\mathrm{0}} \:\:{but}\:\:{A}_{\mathrm{0}} =\:\int_{\mathrm{0}} ^{\infty} \:{x}\:{e}^{−{x}^{\mathrm{2}} } {dx}\:=\:\left[−\frac{\mathrm{1}}{\mathrm{2}}{e}^{−{x}^{\mathrm{2}} } \right]_{\mathrm{0}} ^{\infty} \:\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$${A}_{{n}} =\:\frac{{n}!}{\mathrm{2}}\:. \\ $$
