Question Number 92938 by mathmax by abdo last updated on 09/May/20
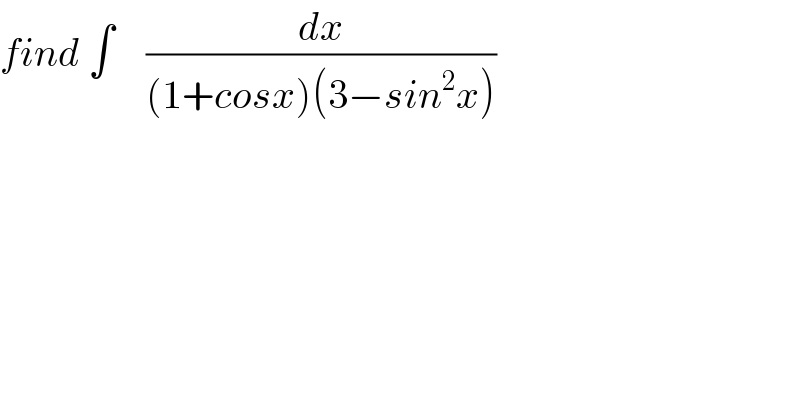
$${find}\:\int\:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{cosx}\right)\left(\mathrm{3}−{sin}^{\mathrm{2}} {x}\right)} \\ $$
Answered by niroj last updated on 10/May/20
![∫(((1−cos x)dx)/((1−cos^2 x)(3−sin^2 x))) = ∫ (1/(sin^2 x(3−sin^2 x)))dx−∫ (( cos xdx)/(sin^2 x(3−sin^2 x))) I= I_1 +I_2 I_1 = ∫ ((sec^2 xdx)/(tan^2 x(3−1+cos^2 x))) = ∫ ((sec^2 xdx)/(tan^2 x(2+(1/(sec^2 x))))) = ∫ ((sec^2 xdx)/(tan^2 x(2+(1/(tan^2 x+1))))) put , tan x=t sec^2 xdx=dt ∫ (( dt)/(t^2 (2+(1/(t^2 +1))))) = ∫ (( dt)/(t^2 (((2t^2 +2+1)/(t^2 +1))))) = ∫ ((t^2 +1)/(t^2 (2t^2 +3)))dt I_k = ∫ (1/(2t^2 +3))dt +∫ (1/(t^2 (2t^2 +3)))dt I_k =I_a +I_b I_a =∫(1/(2t^2 +3))dt= ∫ (1/(((√2) t)^2 +((√3) )^2 ))dt = (1/(2(√3))). (1/( (√2))) tan^(−1) (( t(√2))/( (√3)))+c = (1/(2(√6))) tan^(−1) (((tan x(√2))/( (√3))))+c (A/t^2 )+ (B/(2t^2 +3)) 2t^2 A+3A+t^2 B=1 2t^2 A+t^2 B=0 2A+B=0....(i) 3A=1 A=(1/3)// B=−2A=−(2/3) I_b = (1/3)∫(( 1)/t^2 )dt −(2/3)∫ (1/(2t^2 +3))dt (1/3)[(t^(−2+1) /(−2+1))] −(2/3)∫ (1/(((√2) t)^2 +((√3) )^2 ))dt = (1/3)[−(1/t)]−(2/3)[ (1/(2(√3))).(1/( (√2)))tan^(−1) ((t(√2))/( (√3)))] =−(1/(3t)) −(1/(3(√6))) tan^(−1) ((t(√2))/3) I_k = I_a +I_b I_1 =I_k I_1 =(1/(2(√6))) tan^(−1) (((tanx(√2))/( (√3))))−(1/(3tan x)) −(1/(3(√6))) tan^(−1) ((tan x(√2))/3)+C now, I_2 =−∫ (( cos xdx)/(sin^2 x(3−sin^2 x))) Put, sin x= t cos xdx=dt = −∫ (( dt)/(t^2 (3−t^2 )))= ∫ (dt/(t^2 (t^2 −3))) (A/t^2 )+ (B/(t^2 −3)) At^2 −3A+Bt^2 =1 A+B=0...(i) −3A=1 A=−(1/3) B= −A= (1/3) −(1/3)∫ (1/t^2 )dt +(1/3)∫(1/(t^2 −3))dt −(1/3)((t^(−2+1) /(−2+1)))+(1/3)∫ (1/((t)^2 −((√3) )^2 ))dt −(1/3).(t^(−1) /((−1)))+(1/3).(1/(2(√3)))log ((t−(√3))/(t+(√3)))+C (1/(3t)) +(1/(6(√3)))log ((t−(√3))/(t+(√3)))+C I_2 = (1/(3sin x))+ (1/(6(√3))) log ((sinx−(√3))/(sinx+(√3)))+C complete Integral I=I_1 +I_2 = (1/(2(√6)))tan^(−1) (((tan x(√2))/( (√3))))−(1/(3tan x)) −(1/(3(√6)))tan^(−1) (((tan x(√2))/3))+(1/(3sinx))+(1/(6(√3)))log ((sinx−(√3))/(sinx+(√3))) +C](https://www.tinkutara.com/question/Q92999.png)
$$ \\ $$$$\:\:\int\frac{\left(\mathrm{1}−\mathrm{cos}\:\mathrm{x}\right)\mathrm{dx}}{\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{3}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)} \\ $$$$\:=\:\:\:\int\:\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \mathrm{x}\left(\mathrm{3}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)}\mathrm{dx}−\int\:\frac{\:\mathrm{cos}\:\mathrm{xdx}}{\mathrm{sin}^{\mathrm{2}} \mathrm{x}\left(\mathrm{3}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)} \\ $$$$\:\mathrm{I}=\:{I}_{\mathrm{1}} +{I}_{\mathrm{2}} \\ $$$$\:\:{I}_{\mathrm{1}} \:=\:\int\:\frac{\mathrm{sec}^{\mathrm{2}} \mathrm{xdx}}{\mathrm{tan}^{\mathrm{2}} \mathrm{x}\left(\mathrm{3}−\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)} \\ $$$$\:\:=\:\int\:\frac{\mathrm{sec}^{\mathrm{2}} \mathrm{xdx}}{\mathrm{tan}^{\mathrm{2}} \mathrm{x}\left(\mathrm{2}+\frac{\mathrm{1}}{\mathrm{sec}^{\mathrm{2}} \mathrm{x}}\right)} \\ $$$$\:\:=\:\int\:\frac{\mathrm{sec}^{\mathrm{2}} \mathrm{xdx}}{\mathrm{tan}^{\mathrm{2}} \mathrm{x}\left(\mathrm{2}+\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \mathrm{x}+\mathrm{1}}\right)} \\ $$$$\mathrm{put}\:,\:\mathrm{tan}\:\mathrm{x}=\mathrm{t} \\ $$$$\:\:\:\:\mathrm{sec}^{\mathrm{2}} \mathrm{xdx}=\mathrm{dt} \\ $$$$\:\:\int\:\:\frac{\:\:\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \left(\mathrm{2}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}\right)} \\ $$$$=\:\int\:\frac{\:\:\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \left(\frac{\mathrm{2t}^{\mathrm{2}} +\mathrm{2}+\mathrm{1}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}\right)} \\ $$$$\:=\:\int\:\:\frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \left(\mathrm{2t}^{\mathrm{2}} +\mathrm{3}\right)}\mathrm{dt} \\ $$$$\:{I}_{{k}} =\:\int\:\frac{\mathrm{1}}{\mathrm{2t}^{\mathrm{2}} +\mathrm{3}}\mathrm{dt}\:+\int\:\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \left(\mathrm{2t}^{\mathrm{2}} +\mathrm{3}\right)}\mathrm{dt} \\ $$$$\:\:{I}_{{k}} ={I}_{{a}} +{I}_{{b}} \\ $$$$\:\:{I}_{{a}} =\int\frac{\mathrm{1}}{\mathrm{2t}^{\mathrm{2}} +\mathrm{3}}\mathrm{dt}=\:\int\:\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}}\:\mathrm{t}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\:\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}.\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\mathrm{tan}^{−\mathrm{1}} \frac{\:\mathrm{t}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}+\mathrm{c} \\ $$$$\:\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{6}}}\:\mathrm{tan}^{−\mathrm{1}} \:\left(\frac{\mathrm{tan}\:\mathrm{x}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}\right)+\mathrm{c} \\ $$$$\:\: \\ $$$$\:\:\:\frac{\mathrm{A}}{\mathrm{t}^{\mathrm{2}} }+\:\frac{\mathrm{B}}{\mathrm{2t}^{\mathrm{2}} +\mathrm{3}} \\ $$$$\:\:\mathrm{2t}^{\mathrm{2}} \mathrm{A}+\mathrm{3A}+\mathrm{t}^{\mathrm{2}} \mathrm{B}=\mathrm{1} \\ $$$$\:\:\mathrm{2t}^{\mathrm{2}} \mathrm{A}+\mathrm{t}^{\mathrm{2}} \mathrm{B}=\mathrm{0} \\ $$$$\:\mathrm{2A}+\mathrm{B}=\mathrm{0}….\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\mathrm{3A}=\mathrm{1}\:\: \\ $$$$\:\:\:\:\:\mathrm{A}=\frac{\mathrm{1}}{\mathrm{3}}// \\ $$$$\:\:\:\mathrm{B}=−\mathrm{2}{A}=−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\:{I}_{{b}} =\:\:\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\:\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:−\frac{\mathrm{2}}{\mathrm{3}}\int\:\frac{\mathrm{1}}{\mathrm{2t}^{\mathrm{2}} +\mathrm{3}}\mathrm{dt} \\ $$$$\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{3}}\left[\frac{\mathrm{t}^{−\mathrm{2}+\mathrm{1}} }{−\mathrm{2}+\mathrm{1}}\right]\:−\frac{\mathrm{2}}{\mathrm{3}}\int\:\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}}\:\mathrm{t}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{3}}\left[−\frac{\mathrm{1}}{\mathrm{t}}\right]−\frac{\mathrm{2}}{\mathrm{3}}\left[\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{t}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3t}}\:−\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{6}}}\:\mathrm{tan}\:^{−\mathrm{1}} \:\frac{\mathrm{t}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$$\:{I}_{{k}} =\:{I}_{{a}} +{I}_{{b}} \\ $$$$\:{I}_{\mathrm{1}} ={I}_{{k}} \\ $$$$\:{I}_{\mathrm{1}} \:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{6}}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{tanx}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}\right)−\frac{\mathrm{1}}{\mathrm{3tan}\:\mathrm{x}}\:−\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{6}}}\:\mathrm{tan}^{−\mathrm{1}} \:\frac{\mathrm{tan}\:\mathrm{x}\sqrt{\mathrm{2}}}{\mathrm{3}}+{C} \\ $$$$\:\mathrm{now}, \\ $$$$\:\:{I}_{\mathrm{2}} \:=−\int\:\frac{\:\mathrm{cos}\:\mathrm{xdx}}{\mathrm{sin}^{\mathrm{2}} \mathrm{x}\left(\mathrm{3}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)} \\ $$$$\:\:\:\mathrm{Put},\:\:\mathrm{sin}\:\mathrm{x}=\:\mathrm{t} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\mathrm{xdx}=\mathrm{dt} \\ $$$$\:\:\:\:=\:−\int\:\frac{\:\:\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \left(\mathrm{3}−\mathrm{t}^{\mathrm{2}} \right)}=\:\int\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \left(\mathrm{t}^{\mathrm{2}} −\mathrm{3}\right)} \\ $$$$\:\:\frac{{A}}{{t}^{\mathrm{2}} }+\:\frac{{B}}{{t}^{\mathrm{2}} −\mathrm{3}} \\ $$$$\:\:{At}^{\mathrm{2}} −\mathrm{3}{A}+{Bt}^{\mathrm{2}} =\mathrm{1} \\ $$$$\:\:{A}+{B}=\mathrm{0}…\left({i}\right) \\ $$$$\:\:\:\:\:−\mathrm{3}{A}=\mathrm{1} \\ $$$$\:\:\:\:\:{A}=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\:\:{B}=\:−{A}=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\:\:−\frac{\mathrm{1}}{\mathrm{3}}\int\:\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:+\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\mathrm{3}}\mathrm{dt} \\ $$$$\:\:\:−\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{t}^{−\mathrm{2}+\mathrm{1}} }{−\mathrm{2}+\mathrm{1}}\right)+\frac{\mathrm{1}}{\mathrm{3}}\int\:\frac{\mathrm{1}}{\left(\mathrm{t}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\:\:−\frac{\mathrm{1}}{\mathrm{3}}.\frac{\mathrm{t}^{−\mathrm{1}} }{\left(−\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{3}}.\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{log}\:\frac{\mathrm{t}−\sqrt{\mathrm{3}}}{\mathrm{t}+\sqrt{\mathrm{3}}}+\mathrm{C} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{3t}}\:\:+\frac{\mathrm{1}}{\mathrm{6}\sqrt{\mathrm{3}}}\mathrm{log}\:\frac{\mathrm{t}−\sqrt{\mathrm{3}}}{\mathrm{t}+\sqrt{\mathrm{3}}}+\mathrm{C} \\ $$$$\:\:\:{I}_{\mathrm{2}} =\:\frac{\mathrm{1}}{\mathrm{3sin}\:\mathrm{x}}+\:\frac{\mathrm{1}}{\mathrm{6}\sqrt{\mathrm{3}}}\:\mathrm{log}\:\frac{\mathrm{sinx}−\sqrt{\mathrm{3}}}{\mathrm{sinx}+\sqrt{\mathrm{3}}}+\mathrm{C} \\ $$$$\:\:\:\:\:\:{complete}\:{Integral}\: \\ $$$$\:\:{I}={I}_{\mathrm{1}} +{I}_{\mathrm{2}} \\ $$$$\:\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{6}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:\mathrm{x}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}\right)−\frac{\mathrm{1}}{\mathrm{3tan}\:\mathrm{x}}\:−\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{6}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:\mathrm{x}\sqrt{\mathrm{2}}}{\mathrm{3}}\right)+\frac{\mathrm{1}}{\mathrm{3sinx}}+\frac{\mathrm{1}}{\mathrm{6}\sqrt{\mathrm{3}}}\mathrm{log}\:\frac{\mathrm{sinx}−\sqrt{\mathrm{3}}}{\mathrm{sinx}+\sqrt{\mathrm{3}}}\:+\mathrm{C} \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 10/May/20
��
Commented by peter frank last updated on 10/May/20

$${good} \\ $$
