Question Number 61748 by maxmathsup by imad last updated on 08/Jun/19
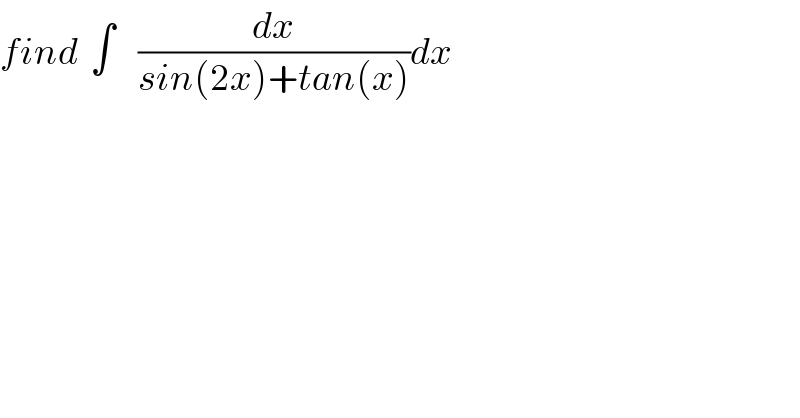
$${find}\:\:\int\:\:\:\:\frac{{dx}}{{sin}\left(\mathrm{2}{x}\right)+{tan}\left({x}\right)}{dx} \\ $$
Commented by Prithwish sen last updated on 08/Jun/19
![∫(dx/(((2tanx)/(1+tan^2 x)) + tanx)) =∫((sec^2 x dx)/(tanx(3+tan^2 x))) put tanx=t =∫(dt/(t(3+t^2 ))) =(1/3)∫[(1/t)−(t/(3+t^2 ))]dt =(1/3)ln((tax)/( (√(3+tan^2 x)))) +C](https://www.tinkutara.com/question/Q61766.png)
$$\int\frac{\mathrm{dx}}{\frac{\mathrm{2tanx}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}}\:+\:\mathrm{tanx}} \\ $$$$=\int\frac{\mathrm{sec}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx}}{\mathrm{tanx}\left(\mathrm{3}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)} \\ $$$$\mathrm{put}\:\mathrm{tanx}=\mathrm{t} \\ $$$$=\int\frac{\mathrm{dt}}{\mathrm{t}\left(\mathrm{3}+\mathrm{t}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int\left[\frac{\mathrm{1}}{\mathrm{t}}−\frac{\mathrm{t}}{\mathrm{3}+\mathrm{t}^{\mathrm{2}} }\right]\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\frac{\mathrm{tax}}{\:\sqrt{\mathrm{3}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}}}\:+\mathrm{C} \\ $$$$ \\ $$
