Question Number 22232 by tapan das last updated on 13/Oct/17
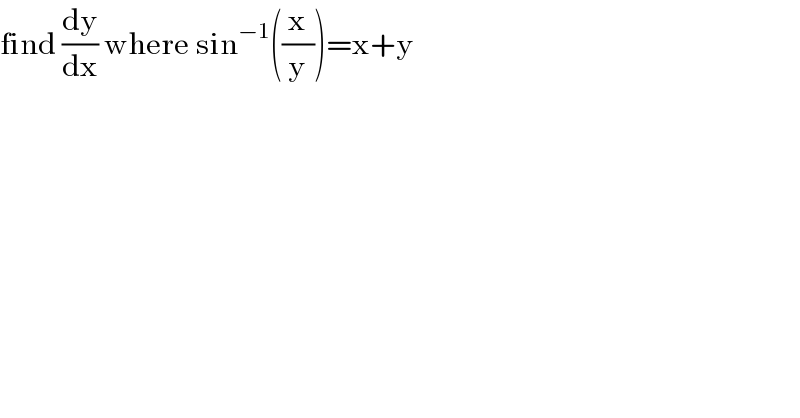
$$\mathrm{find}\:\frac{\mathrm{dy}}{\mathrm{dx}}\:\mathrm{where}\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{y}}\right)=\mathrm{x}+\mathrm{y} \\ $$
Answered by ajfour last updated on 13/Oct/17
![x=ysin (x+y) 1=(dy/dx)sin (x+y)+y(1+(dy/dx))cos (x+y) (dy/dx)[sin (x+y)+ycos (x+y)]= 1−ycos (x+y) (dy/dx)=((1−ycos (x+y))/(sin (x+y)+ycos (x+y))) .](https://www.tinkutara.com/question/Q22235.png)
$$\:\:\:\:\:{x}={y}\mathrm{sin}\:\left({x}+{y}\right) \\ $$$$\:\:\:\:\mathrm{1}=\frac{{dy}}{{dx}}\mathrm{sin}\:\left({x}+{y}\right)+{y}\left(\mathrm{1}+\frac{{dy}}{{dx}}\right)\mathrm{cos}\:\left({x}+{y}\right) \\ $$$$\:\:\:\:\:\frac{{dy}}{{dx}}\left[\mathrm{sin}\:\left({x}+{y}\right)+{y}\mathrm{cos}\:\left({x}+{y}\right)\right]= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}−{y}\mathrm{cos}\:\left({x}+{y}\right) \\ $$$$\:\:\:\:\:\frac{{dy}}{{dx}}=\frac{\mathrm{1}−{y}\mathrm{cos}\:\left({x}+{y}\right)}{\mathrm{sin}\:\left({x}+{y}\right)+{y}\mathrm{cos}\:\left({x}+{y}\right)}\:. \\ $$
