Question Number 39483 by math khazana by abdo last updated on 06/Jul/18
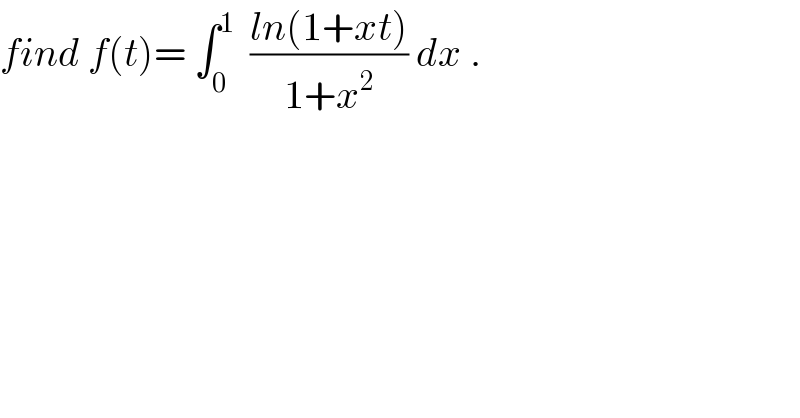
$${find}\:{f}\left({t}\right)=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left(\mathrm{1}+{xt}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:. \\ $$
Commented by math khazana by abdo last updated on 07/Jul/18
![we have f(t) =∫_0 ^1 ((ln(1+tx))/(1+x^2 ))dx ⇒ f^′ (t) = ∫_0 ^1 (x/((1+tx)(1+x^2 )))dx f^′ (x)=(1/t) ∫_0 ^1 ((1+tx−1)/((1+tx)(1+x^2 )))dx =(1/t) ∫_0 ^1 (dx/(1+x^2 )) −(1/t) ∫_0 ^1 (dx/((1+tx)(1+x^2 ))) =(π/(2t)) −(1/t) ∫_0 ^1 (dx/((1+tx)(1+x^2 ))) let decompose F(x) = (1/((1+tx)(1+x^2 ))) F(x) = (a/(tx+1)) +((bx +c)/(x^2 +1)) a=lim_(x→−(1/t)) (tx+1)F(x)= (1/(1+(1/t^2 ))) =(t^2 /(t^2 +1)) lim_(x→+∞) xF(x)= (a/t) +b=0 ⇒b=−(a/t) =−(t/(t^2 +1)) F(0) =a +c =1 ⇒c=1−a =1−(t^2 /(t^2 +1))=(1/(t^2 +1)) ⇒ F(x)= (t^2 /(t^2 +1)) .(1/(tx+1)) +((((−t)/(t^2 +1))x +(1/(t^2 +1)))/(x^2 +1)) = (t^2 /((t^2 +1)(tx+1))) −(1/(t^2 +1)) ((tx−1)/(x^2 +1)) ⇒ ∫_0 ^1 F(x)dx =(t/(t^2 +1)) ∫_0 ^1 (t/(tx+1))dx −(t/(2(t^2 +1)))∫_0 ^1 ((2x)/(x^2 +1))dx +(1/(t^2 +1)) ∫_0 ^1 (dx/(x^2 +1)) =(t/(t^2 +1))[ln∣tx+1∣]_0 ^1 −(t/(2(t^2 +1)))[ln(x^2 +1)]_0 ^1 + (1/(t^2 +1)) [arctanx]_0 ^1 = (t/(t^2 +1))ln∣t+1∣ −((ln(2))/2) (t/(t^2 +1)) +(π/(4(t^2 +1))) ⇒ f^′ (t)=(π/(2t)) −((ln∣t+1∣)/(t^2 +1)) +((ln(2))/(2(t^2 +1))) −(π/(4t(t^2 +1))) ⇒ if we suppose t>0 we get f(t) =(π/2)ln(t) −∫_1 ^t ((ln(1+x))/(x^2 +1))dx+((ln(2))/2) ∫_1 ^t (dx/(x^2 +1)) −(π/4) ∫_1 ^t (dx/(x(x^2 +1))) +c =(π/2)ln(t) −∫_1 ^t ((ln(1+x))/(x^2 +1))dx +((ln(2))/2)( arctant −(π/4)) −(π/4) ∫_1 ^t ( (1/x) −(x/(1+x^2 )))dx +c =(π/2)ln(t) −∫_1 ^t ((ln(1+x))/(x^2 +1))dx +((ln(2))/2){arctan(t)−(π/4)} −(π/4)ln(t) +(π/8) ∫_1 ^t ((2x)/(1+x^2 ))dx +c =(π/4)ln(t) −∫_1 ^t ((ln(1+x))/(x^2 +1))dx +((ln(2))/2){arctan(t)−(π/4)} +(π/8){ln(1+t^2 ) −ln(2)} +c](https://www.tinkutara.com/question/Q39538.png)
$${we}\:{have}\:{f}\left({t}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{tx}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:\Rightarrow \\ $$$${f}^{'} \left({t}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{x}}{\left(\mathrm{1}+{tx}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}\: \\ $$$${f}^{'} \left({x}\right)=\frac{\mathrm{1}}{{t}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{1}+{tx}−\mathrm{1}}{\left(\mathrm{1}+{tx}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx} \\ $$$$=\frac{\mathrm{1}}{{t}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\:−\frac{\mathrm{1}}{{t}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dx}}{\left(\mathrm{1}+{tx}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$$$=\frac{\pi}{\mathrm{2}{t}}\:−\frac{\mathrm{1}}{{t}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dx}}{\left(\mathrm{1}+{tx}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:{let}\:{decompose} \\ $$$${F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\left(\mathrm{1}+{tx}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$$${F}\left({x}\right)\:=\:\frac{{a}}{{tx}+\mathrm{1}}\:\:+\frac{{bx}\:+{c}}{{x}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}={lim}_{{x}\rightarrow−\frac{\mathrm{1}}{{t}}} \:\:\left({tx}+\mathrm{1}\right){F}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}\:=\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${lim}_{{x}\rightarrow+\infty} \:{xF}\left({x}\right)=\:\frac{{a}}{{t}}\:+{b}=\mathrm{0}\:\Rightarrow{b}=−\frac{{a}}{{t}}\:=−\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)\:={a}\:+{c}\:=\mathrm{1}\:\Rightarrow{c}=\mathrm{1}−{a}\:=\mathrm{1}−\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} \:+\mathrm{1}}=\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${F}\left({x}\right)=\:\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} \:+\mathrm{1}}\:.\frac{\mathrm{1}}{{tx}+\mathrm{1}}\:+\frac{\frac{−{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}{x}\:+\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}}{{x}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\:\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\left({tx}+\mathrm{1}\right)}\:\:−\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\frac{{tx}−\mathrm{1}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{F}\left({x}\right){dx}\:=\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{t}}{{tx}+\mathrm{1}}{dx}\:−\frac{{t}}{\mathrm{2}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx} \\ $$$$+\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\left[{ln}\mid{tx}+\mathrm{1}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:\:−\frac{{t}}{\mathrm{2}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\left[{ln}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$+\:\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\left[{arctanx}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\:\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}{ln}\mid{t}+\mathrm{1}\mid\:\:\:−\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\:+\frac{\pi}{\mathrm{4}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow \\ $$$${f}^{'} \left({t}\right)=\frac{\pi}{\mathrm{2}{t}}\:−\frac{{ln}\mid{t}+\mathrm{1}\mid}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\:+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:−\frac{\pi}{\mathrm{4}{t}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow \\ $$$${if}\:{we}\:{suppose}\:{t}>\mathrm{0}\:{we}\:{get} \\ $$$${f}\left({t}\right)\:=\frac{\pi}{\mathrm{2}}{ln}\left({t}\right)\:−\int_{\mathrm{1}} ^{{t}} \:\:\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:\int_{\mathrm{1}} ^{{t}} \:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$−\frac{\pi}{\mathrm{4}}\:\int_{\mathrm{1}} ^{{t}} \:\:\:\:\frac{{dx}}{{x}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:+{c} \\ $$$$=\frac{\pi}{\mathrm{2}}{ln}\left({t}\right)\:−\int_{\mathrm{1}} ^{{t}} \:\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\left(\:{arctant}\:−\frac{\pi}{\mathrm{4}}\right) \\ $$$$−\frac{\pi}{\mathrm{4}}\:\int_{\mathrm{1}} ^{{t}} \left(\:\frac{\mathrm{1}}{{x}}\:−\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\right){dx}\:+{c} \\ $$$$=\frac{\pi}{\mathrm{2}}{ln}\left({t}\right)\:−\int_{\mathrm{1}} ^{{t}} \:\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\left\{{arctan}\left({t}\right)−\frac{\pi}{\mathrm{4}}\right\} \\ $$$$−\frac{\pi}{\mathrm{4}}{ln}\left({t}\right)\:\:+\frac{\pi}{\mathrm{8}}\:\int_{\mathrm{1}} ^{{t}} \:\:\:\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:+{c} \\ $$$$=\frac{\pi}{\mathrm{4}}{ln}\left({t}\right)\:−\int_{\mathrm{1}} ^{{t}} \:\:\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\left\{{arctan}\left({t}\right)−\frac{\pi}{\mathrm{4}}\right\} \\ $$$$+\frac{\pi}{\mathrm{8}}\left\{{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\:−{ln}\left(\mathrm{2}\right)\right\}\:+{c} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by math khazana by abdo last updated on 07/Jul/18
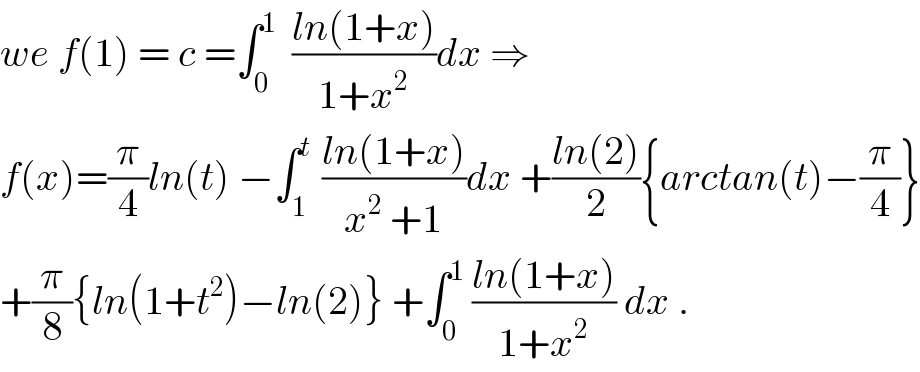
$${we}\:{f}\left(\mathrm{1}\right)\:=\:{c}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:\Rightarrow \\ $$$${f}\left({x}\right)=\frac{\pi}{\mathrm{4}}{ln}\left({t}\right)\:−\int_{\mathrm{1}} ^{{t}} \:\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\left\{{arctan}\left({t}\right)−\frac{\pi}{\mathrm{4}}\right\} \\ $$$$+\frac{\pi}{\mathrm{8}}\left\{{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)−{ln}\left(\mathrm{2}\right)\right\}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:. \\ $$
Commented by math khazana by abdo last updated on 07/Jul/18

$${f}\left({t}\right)=… \\ $$
