Question Number 44472 by abdo.msup.com last updated on 29/Sep/18
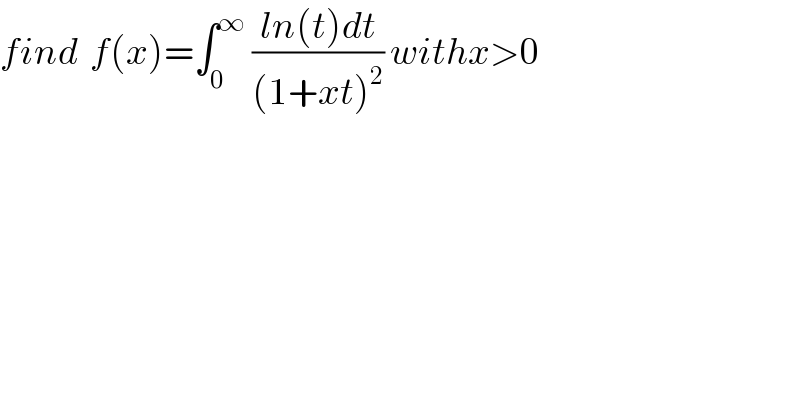
$${find}\:\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left({t}\right){dt}}{\left(\mathrm{1}+{xt}\right)^{\mathrm{2}} }\:{withx}>\mathrm{0} \\ $$
Commented by maxmathsup by imad last updated on 30/Sep/18
![changement xt =u give f(x) =∫_0 ^∞ ((ln((u/x)))/((1+u)^2 )) (du/x) =(1/x)∫_0 ^∞ ((ln(u)−ln(x))/((1+u)^2 ))du =(1/x)∫_0 ^∞ ((ln(u))/((1+u)^2 )) du −((ln(x))/x) ∫_0 ^∞ (du/((1+u)^2 )) =0 −((ln(x))/x) [−(1/(1+u))]_0 ^(+∞) =−((ln(x))/x) ⇒f(x) =−((ln(x))/x) .](https://www.tinkutara.com/question/Q44514.png)
$${changement}\:{xt}\:={u}\:{give}\: \\ $$$${f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left(\frac{{u}}{{x}}\right)}{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} }\:\frac{{du}}{{x}}\:=\frac{\mathrm{1}}{{x}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{ln}\left({u}\right)−{ln}\left({x}\right)}{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} }{du} \\ $$$$=\frac{\mathrm{1}}{{x}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left({u}\right)}{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} }\:{du}\:−\frac{{ln}\left({x}\right)}{{x}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{du}}{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{0}\:−\frac{{ln}\left({x}\right)}{{x}}\:\left[−\frac{\mathrm{1}}{\mathrm{1}+{u}}\right]_{\mathrm{0}} ^{+\infty} \:=−\frac{{ln}\left({x}\right)}{{x}}\:\Rightarrow{f}\left({x}\right)\:=−\frac{{ln}\left({x}\right)}{{x}}\:. \\ $$$$ \\ $$
