Question Number 65445 by mathmax by abdo last updated on 30/Jul/19
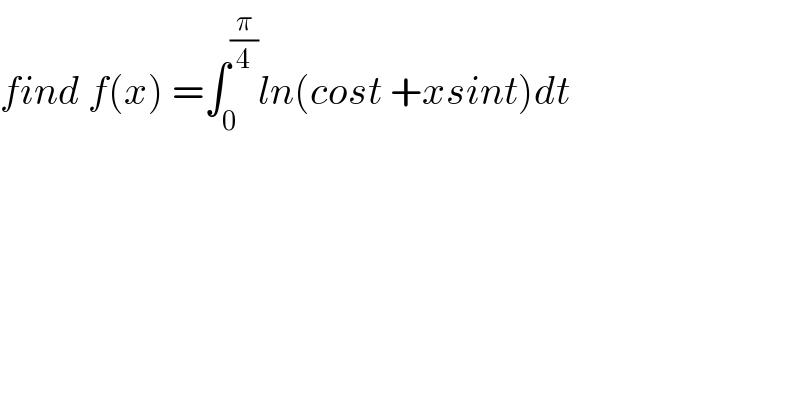
$${find}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cost}\:+{xsint}\right){dt}\:\:\: \\ $$
Commented by Prithwish sen last updated on 30/Jul/19
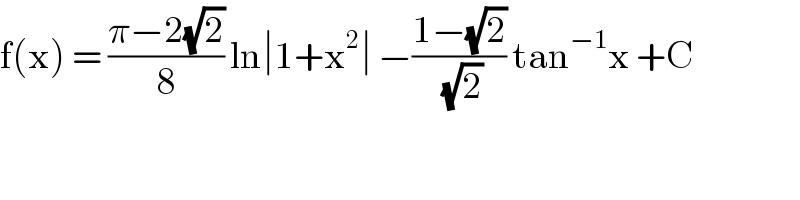
$$\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\pi−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{8}}\:\mathrm{ln}\mid\mathrm{1}+\mathrm{x}^{\mathrm{2}} \mid\:−\frac{\mathrm{1}−\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}}\:\mathrm{tan}^{−\mathrm{1}} \mathrm{x}\:+\mathrm{C} \\ $$
Commented by mathmax by abdo last updated on 31/Jul/19
![we have f^′ (x) =∫_0 ^(π/4) ((sint)/(cost +xsint)) dt changement tan((t/2)) =u give f^′ (x) =∫_0 ^((√2)−1) (((2u)/(1+u^2 ))/(((1−u^2 )/(1+u^2 )) +x((2u)/(1+u^2 )))) ((2du)/(1+u^2 )) =∫_0 ^((√2)−1) ((4u)/((1+u^2 )(1−u^2 +2xu)))du =−4 ∫_0 ^((√2)−1) ((udu)/((u^2 +1)(u^2 −2xu−1))) let decompose F(u) =(u/((u^2 +1)(u^2 −2xu−1))) u^2 −2xu−1 =0 →Δ^′ =x^2 +1 ⇒u_1 =x+(√(1+x^2 )) and u_2 =x−(√(1+x^2 )) F(u) =(u/((u^2 +1)(u−u_1 )(u−u_2 ))) =(a/(u−u_1 )) +(b/(u−u_2 )) +((cu +d)/(u^2 +1)) a =(u_1 /((u_1 ^2 +1)(u_1 −u_2 ))) =((x+(√(1+x^2 )))/((1+(x+(√(1+x^2 )))^2 2(√(1+x^2 )))) b =(u_2 /((1+u_2 ^2 )(u_2 −u_1 ))) =((x−(√(1+x^2 )))/((1+(x−(√(1+x^2 )))^2 (−2(√(1+x^2 ))))) lim_(u→+∞) uF(u) =0 =a+b +c ⇒c =−a−b ⇒ F(u) =(a/(u−u_1 ))+(b/(u−u_2 )) +(((−a−b)u +d)/(u^2 +1)) F(0)=0 =−(a/u_1 )−(b/u_2 ) +d ⇒d =(a/u_1 )+(b/u_2 ) ⇒ f^′ (x) =−4 ∫_0 ^((√2)−1) ((a/(u−u_1 )) +(b/(u−u_2 )) +((cu+d)/(u^2 +1)))du =−4 [aln∣u−u_1 ∣+bln∣u−u_2 ∣]_0 ^((√2)−1) −4 { (1/2)∫_0 ^((√2)−1) ((2cu +2d)/(u^2 +1))du} =−4{aln∣(√2)−1−u_1 ∣+bln∣(√2)−1−u_2 ∣−aln∣u_1 ∣−bln∣u_2 ∣} 2 { c[ln(u^2 +1)]_0 ^((√2)−1) +2d [arctanu]_0 ^((√2)−1) =.... be continued....](https://www.tinkutara.com/question/Q65501.png)
$${we}\:{have}\:{f}^{'} \left({x}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{{sint}}{{cost}\:+{xsint}}\:{dt}\:\:{changement}\:{tan}\left(\frac{{t}}{\mathrm{2}}\right)\:={u}\:{give} \\ $$$${f}^{'} \left({x}\right)\:=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\frac{\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}{\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }\:+{x}\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{\mathrm{4}{u}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}−{u}^{\mathrm{2}} \:+\mathrm{2}{xu}\right)}{du} \\ $$$$=−\mathrm{4}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\frac{{udu}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left({u}^{\mathrm{2}} −\mathrm{2}{xu}−\mathrm{1}\right)}\:{let}\:{decompose}\: \\ $$$${F}\left({u}\right)\:=\frac{{u}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left({u}^{\mathrm{2}} −\mathrm{2}{xu}−\mathrm{1}\right)} \\ $$$${u}^{\mathrm{2}} −\mathrm{2}{xu}−\mathrm{1}\:=\mathrm{0}\:\rightarrow\Delta^{'} \:={x}^{\mathrm{2}} +\mathrm{1}\:\Rightarrow{u}_{\mathrm{1}} ={x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\:\:{and}\:{u}_{\mathrm{2}} ={x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$${F}\left({u}\right)\:=\frac{{u}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left({u}−{u}_{\mathrm{1}} \right)\left({u}−{u}_{\mathrm{2}} \right)}\:=\frac{{a}}{{u}−{u}_{\mathrm{1}} }\:+\frac{{b}}{{u}−{u}_{\mathrm{2}} }\:+\frac{{cu}\:+{d}}{{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}\:=\frac{{u}_{\mathrm{1}} }{\left({u}_{\mathrm{1}} ^{\mathrm{2}} \:+\mathrm{1}\right)\left({u}_{\mathrm{1}} −{u}_{\mathrm{2}} \right)}\:=\frac{{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\left(\mathrm{1}+\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} \mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right.} \\ $$$${b}\:=\frac{{u}_{\mathrm{2}} }{\left(\mathrm{1}+{u}_{\mathrm{2}} ^{\mathrm{2}} \right)\left({u}_{\mathrm{2}} −{u}_{\mathrm{1}} \right)}\:=\frac{{x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\left(\mathrm{1}+\left({x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} \left(−\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)\right.} \\ $$$${lim}_{{u}\rightarrow+\infty} {uF}\left({u}\right)\:=\mathrm{0}\:={a}+{b}\:+{c}\:\Rightarrow{c}\:=−{a}−{b}\:\Rightarrow \\ $$$${F}\left({u}\right)\:=\frac{{a}}{{u}−{u}_{\mathrm{1}} }+\frac{{b}}{{u}−{u}_{\mathrm{2}} }\:+\frac{\left(−{a}−{b}\right){u}\:+{d}}{{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)=\mathrm{0}\:=−\frac{{a}}{{u}_{\mathrm{1}} }−\frac{{b}}{{u}_{\mathrm{2}} }\:+{d}\:\Rightarrow{d}\:=\frac{{a}}{{u}_{\mathrm{1}} }+\frac{{b}}{{u}_{\mathrm{2}} }\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)\:=−\mathrm{4}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \left(\frac{{a}}{{u}−{u}_{\mathrm{1}} }\:+\frac{{b}}{{u}−{u}_{\mathrm{2}} }\:+\frac{{cu}+{d}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\right){du} \\ $$$$=−\mathrm{4}\:\left[{aln}\mid{u}−{u}_{\mathrm{1}} \mid+{bln}\mid{u}−{u}_{\mathrm{2}} \mid\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:−\mathrm{4}\:\left\{\:\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\frac{\mathrm{2}{cu}\:+\mathrm{2}{d}}{{u}^{\mathrm{2}} \:+\mathrm{1}}{du}\right\} \\ $$$$=−\mathrm{4}\left\{{aln}\mid\sqrt{\mathrm{2}}−\mathrm{1}−{u}_{\mathrm{1}} \mid+{bln}\mid\sqrt{\mathrm{2}}−\mathrm{1}−{u}_{\mathrm{2}} \mid−{aln}\mid{u}_{\mathrm{1}} \mid−{bln}\mid{u}_{\mathrm{2}} \mid\right\} \\ $$$$\mathrm{2}\:\left\{\:{c}\left[{ln}\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:+\mathrm{2}{d}\:\left[{arctanu}\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:=….\right. \\ $$$${be}\:{continued}…. \\ $$$$ \\ $$
