Question Number 60976 by maxmathsup by imad last updated on 28/May/19
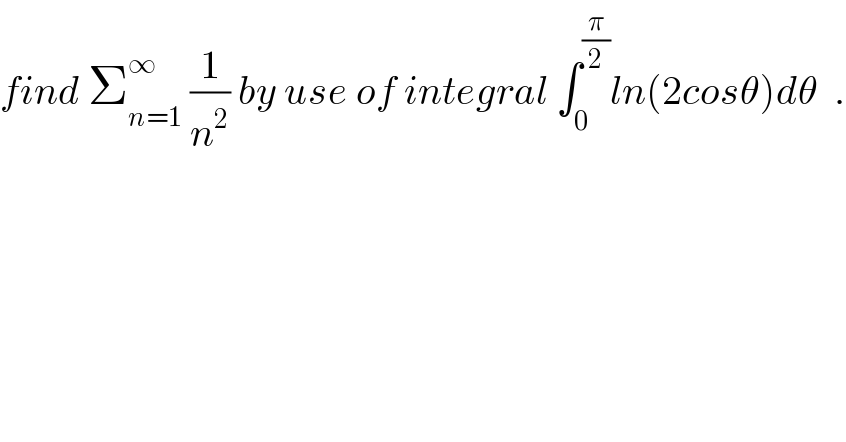
$${find}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:{by}\:{use}\:{of}\:{integral}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{2}{cos}\theta\right){d}\theta\:\:. \\ $$
Commented by maxmathsup by imad last updated on 31/May/19
![we have ∫_0 ^(π/2) ln(2cosθ)dθ =∫_0 ^(π/2) ln(e^(iθ) +e^(−iθ) )dθ =∫_0 ^(π/2) ln{e^(iθ) (1+e^(−2iθ) )}dθ =∫_0 ^(π/2) iθ dθ +∫_0 ^(π/2) ln(1+e^(−2iθ) )dθ =i[(θ^2 /2)]_0 ^(π/2) +∫_0 ^(π/2) ln(1+e^(−2iθ) )dθ =i(π^2 /8) +∫_0 ^(π/2) ln(1+e^(−2iθ) )dθ we have for ∣z∣≤1 ln^′ (1+z) =(1/(1+z)) =Σ_(n=0) ^∞ (−1)^n z^n ⇒ ln(1+z) =Σ_(n=0) ^∞ (((−1)^n z^(n+1) )/(n+1)) +c (c=0) =Σ_(n=1) ^∞ (((−1)^(n−1) z^n )/n) ⇒∫_0 ^(π/2) ln(1+e^(−2iθ) ) =∫_0 ^(π/2) (Σ_(n=1) ^∞ (((−1)^(n−1) e^(−2inθ) )/n))dθ =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) ∫_0 ^(π/2) e^(−2inθ) dθ =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) [−(1/(2in)) e^(−2inθ) ]_0 ^(π/2) =−(1/(2i)) Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 ){ (−1)^n −1} =(1/i) Σ_(n=0) ^∞ (1/((2n+1)^2 )) =−i Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒ ∫_0 ^(π/2) ln(2cosθ)dθ =i((π^2 /8) − Σ_(n=0) ^∞ (1/((2n+1)^2 ))) but this integral is real ⇒(π^2 /8) −Σ_(n=0) ^∞ (1/((2n+1)^2 )) =0 ⇒Σ_(n=0) ^∞ (1/((2n+1)^2 )) =(π^2 /8) we have Σ_(n=1) ^∞ (1/n^2 ) =(1/4) Σ_(n=1) ^∞ (1/n^2 ) +Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒ (3/4) Σ_(n=1) ^∞ (1/n^2 ) =(π^2 /8) ⇒ Σ_(n=1) ^∞ (1/n^2 ) =(4/3)(π^2 /8) =(π^2 /6) .](https://www.tinkutara.com/question/Q61308.png)
$${we}\:{have}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{2}{cos}\theta\right){d}\theta\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({e}^{{i}\theta} \:+{e}^{−{i}\theta} \right){d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left\{{e}^{{i}\theta} \left(\mathrm{1}+{e}^{−\mathrm{2}{i}\theta} \right)\right\}{d}\theta\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {i}\theta\:{d}\theta\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{ln}\left(\mathrm{1}+{e}^{−\mathrm{2}{i}\theta} \right){d}\theta \\ $$$$={i}\left[\frac{\theta^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{1}+{e}^{−\mathrm{2}{i}\theta} \right){d}\theta\:={i}\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{1}+{e}^{−\mathrm{2}{i}\theta} \right){d}\theta \\ $$$${we}\:{have}\:{for}\:\mid{z}\mid\leqslant\mathrm{1}\:{ln}^{'} \left(\mathrm{1}+{z}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+{z}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {z}^{{n}} \:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{z}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} \:{z}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:+{c}\:\:\:\:\:\:\:\:\left({c}=\mathrm{0}\right) \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{z}^{{n}} }{{n}}\:\:\Rightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{1}+{e}^{−\mathrm{2}{i}\theta} \right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {e}^{−\mathrm{2}{in}\theta} }{{n}}\right){d}\theta \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{e}^{−\mathrm{2}{in}\theta} \:{d}\theta \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\left[−\frac{\mathrm{1}}{\mathrm{2}{in}}\:{e}^{−\mathrm{2}{in}\theta} \right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}{i}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} }\left\{\:\:\left(−\mathrm{1}\right)^{{n}} −\mathrm{1}\right\} \\ $$$$=\frac{\mathrm{1}}{{i}}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=−{i}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{2}{cos}\theta\right){d}\theta\:={i}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:−\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\right)\:\:{but}\:{this}\:{integral}\:{is} \\ $$$${real}\:\Rightarrow\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:−\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\mathrm{0}\:\Rightarrow\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$${we}\:{have}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{4}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:+\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\Rightarrow\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\frac{\mathrm{4}}{\mathrm{3}}\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:. \\ $$
