Menu Close

find-solution-set-of-equation-cos-3x-cos-x-x-0-3pi-

Tinku Tara 0 Comments
Pin




Question Number 114272 by bemath last updated on 18/Sep/20
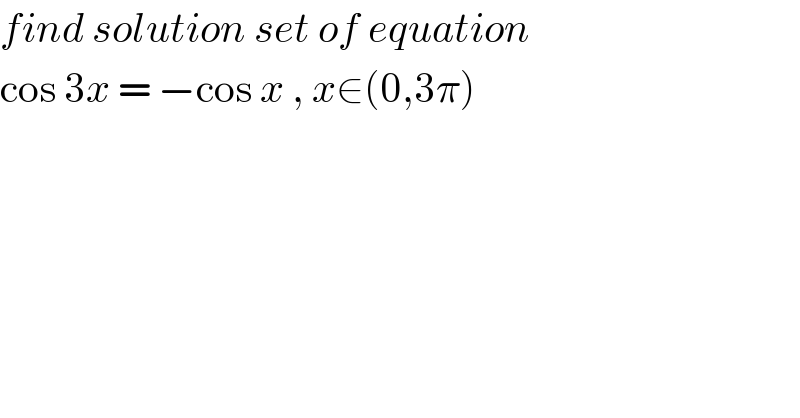
find solution set of equation cos 3x = −cos x , x∈(0,3π)
$${find}\:{solution}\:{set}\:{of}\:{equation}\: \\ $$$$\mathrm{cos}\:\mathrm{3}{x}\:=\:−\mathrm{cos}\:{x}\:,\:{x}\in\left(\mathrm{0},\mathrm{3}\pi\right) \\ $$
Commented by malwaan last updated on 18/Sep/20
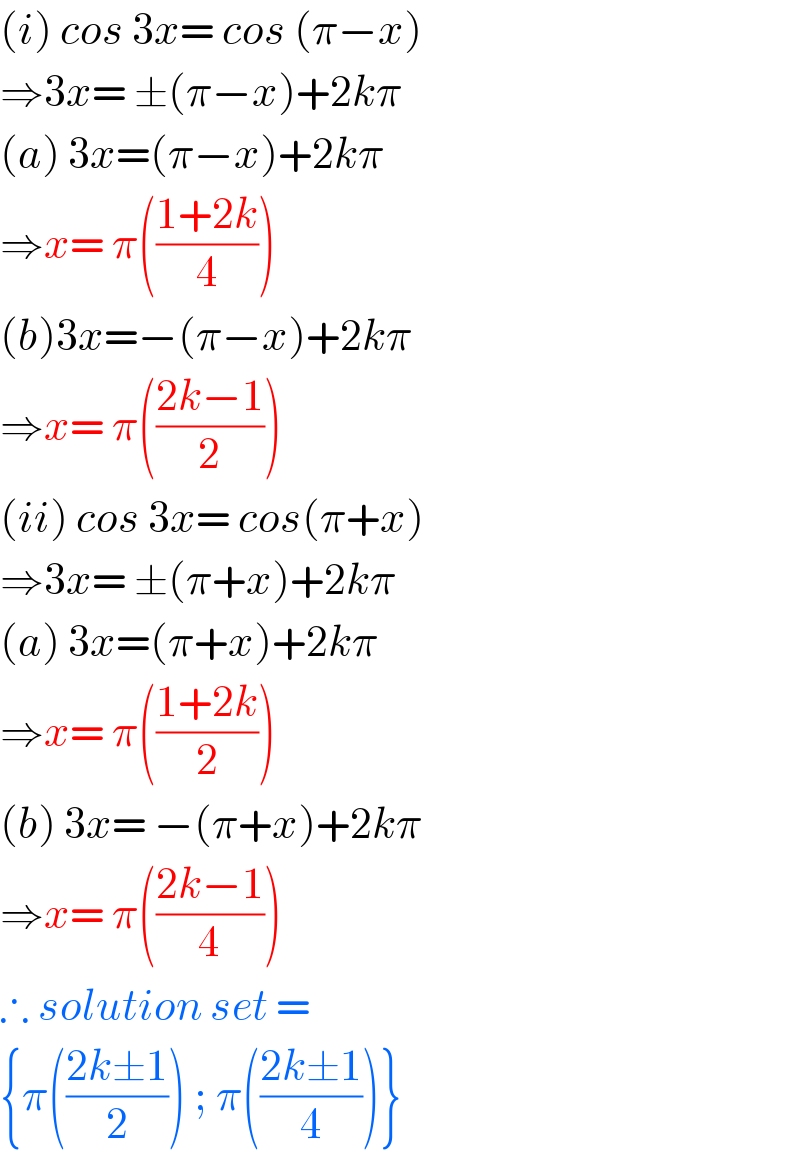
(i) cos 3x= cos (π−x) ⇒3x= ±(π−x)+2kπ (a) 3x=(π−x)+2kπ ⇒x= π(((1+2k)/4)) (b)3x=−(π−x)+2kπ ⇒x= π(((2k−1)/2)) (ii) cos 3x= cos(π+x) ⇒3x= ±(π+x)+2kπ (a) 3x=(π+x)+2kπ ⇒x= π(((1+2k)/2)) (b) 3x= −(π+x)+2kπ ⇒x= π(((2k−1)/4)) ∴ solution set = {π(((2k±1)/2)) ; π(((2k±1)/4))}
$$\left({i}\right)\:{cos}\:\mathrm{3}{x}=\:{cos}\:\left(\pi−{x}\right) \\ $$$$\Rightarrow\mathrm{3}{x}=\:\pm\left(\pi−{x}\right)+\mathrm{2}{k}\pi \\ $$$$\left({a}\right)\:\mathrm{3}{x}=\left(\pi−{x}\right)+\mathrm{2}{k}\pi \\ $$$$\Rightarrow{x}=\:\pi\left(\frac{\mathrm{1}+\mathrm{2}{k}}{\mathrm{4}}\right) \\ $$$$\left({b}\right)\mathrm{3}{x}=−\left(\pi−{x}\right)+\mathrm{2}{k}\pi \\ $$$$\Rightarrow{x}=\:\pi\left(\frac{\mathrm{2}{k}−\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\left({ii}\right)\:{cos}\:\mathrm{3}{x}=\:{cos}\left(\pi+{x}\right) \\ $$$$\Rightarrow\mathrm{3}{x}=\:\pm\left(\pi+{x}\right)+\mathrm{2}{k}\pi \\ $$$$\left({a}\right)\:\mathrm{3}{x}=\left(\pi+{x}\right)+\mathrm{2}{k}\pi \\ $$$$\Rightarrow{x}=\:\pi\left(\frac{\mathrm{1}+\mathrm{2}{k}}{\mathrm{2}}\right) \\ $$$$\left({b}\right)\:\mathrm{3}{x}=\:−\left(\pi+{x}\right)+\mathrm{2}{k}\pi \\ $$$$\Rightarrow{x}=\:\pi\left(\frac{\mathrm{2}{k}−\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\therefore\:{solution}\:{set}\:= \\ $$$$\left\{\pi\left(\frac{\mathrm{2}{k}\pm\mathrm{1}}{\mathrm{2}}\right)\:;\:\pi\left(\frac{\mathrm{2}{k}\pm\mathrm{1}}{\mathrm{4}}\right)\right\} \\ $$
Commented by bemath last updated on 18/Sep/20
hahaha santuy
$${hahaha}\:{santuy} \\ $$
Commented by abdullahquwatan last updated on 18/Sep/20
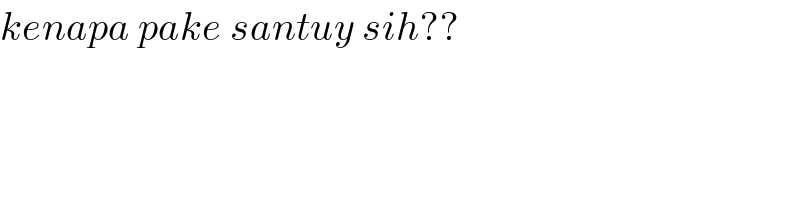
kenapa pake santuy sih??
$${kenapa}\:{pake}\:{santuy}\:{sih}?? \\ $$
Answered by bemath last updated on 18/Sep/20
Answered by malwaan last updated on 18/Sep/20
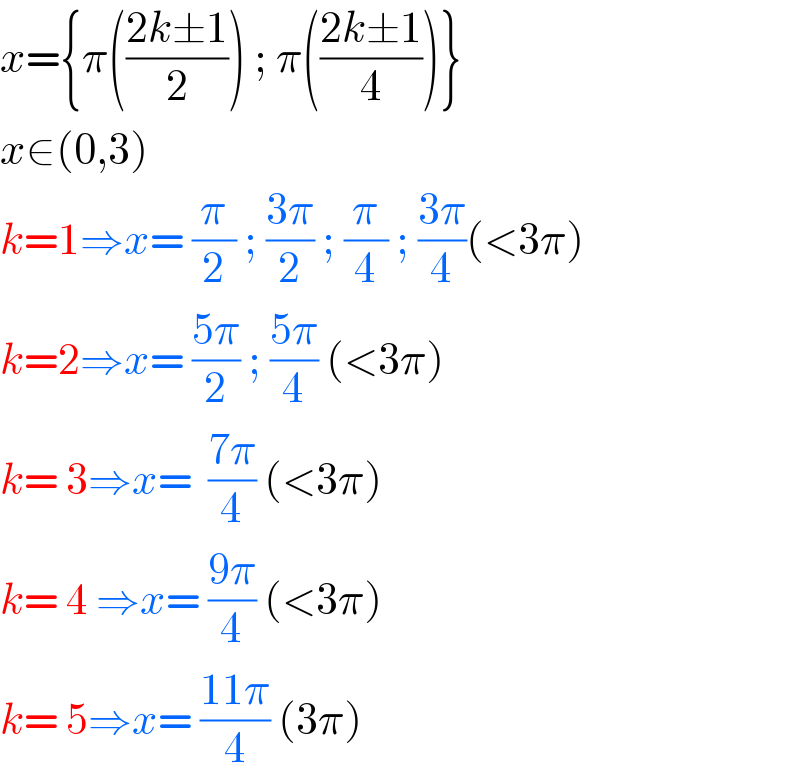
x={π(((2k±1)/2)) ; π(((2k±1)/4))} x∈(0,3) k=1⇒x= (π/2) ; ((3π)/2) ; (π/4) ; ((3π)/4)(<3π) k=2⇒x= ((5π)/2) ; ((5π)/4) (<3π) k= 3⇒x= ((7π)/4) (<3π) k= 4 ⇒x= ((9π)/4) (<3π) k= 5⇒x= ((11π)/4) (3π)
$${x}=\left\{\pi\left(\frac{\mathrm{2}{k}\pm\mathrm{1}}{\mathrm{2}}\right)\:;\:\pi\left(\frac{\mathrm{2}{k}\pm\mathrm{1}}{\mathrm{4}}\right)\right\} \\ $$$${x}\in\left(\mathrm{0},\mathrm{3}\right) \\ $$$${k}=\mathrm{1}\Rightarrow{x}=\:\frac{\pi}{\mathrm{2}}\:;\:\frac{\mathrm{3}\pi}{\mathrm{2}}\:;\:\frac{\pi}{\mathrm{4}}\:;\:\frac{\mathrm{3}\pi}{\mathrm{4}}\left(<\mathrm{3}\pi\right) \\ $$$${k}=\mathrm{2}\Rightarrow{x}=\:\frac{\mathrm{5}\pi}{\mathrm{2}}\:;\:\frac{\mathrm{5}\pi}{\mathrm{4}}\:\left(<\mathrm{3}\pi\right) \\ $$$${k}=\:\mathrm{3}\Rightarrow{x}=\:\:\frac{\mathrm{7}\pi}{\mathrm{4}}\:\left(<\mathrm{3}\pi\right) \\ $$$${k}=\:\mathrm{4}\:\Rightarrow{x}=\:\frac{\mathrm{9}\pi}{\mathrm{4}}\:\left(<\mathrm{3}\pi\right) \\ $$$${k}=\:\mathrm{5}\Rightarrow{x}=\:\frac{\mathrm{11}\pi}{\mathrm{4}}\:\left(\mathrm{3}\pi\right) \\ $$
Answered by Dwaipayan Shikari last updated on 18/Sep/20
cos3x+cosx=0 2cos2xcosx=0 cos2x=0 2x=kπ+(π/2) x=((kπ)/2)+(π/4) or x=kπ+(π/2) (k∈Z) Solution set x∈[(π/4),((3π)/4),((5π)/4),((7π)/4),((9π)/4),((11π)/4)] x∈[(π/2),((3π)/2),((5π)/2)]
$${cos}\mathrm{3}{x}+{cosx}=\mathrm{0} \\ $$$$\mathrm{2}{cos}\mathrm{2}{xcosx}=\mathrm{0} \\ $$$${cos}\mathrm{2}{x}=\mathrm{0} \\ $$$$\mathrm{2}{x}={k}\pi+\frac{\pi}{\mathrm{2}} \\ $$$${x}=\frac{{k}\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{4}} \\ $$$${or} \\ $$$${x}={k}\pi+\frac{\pi}{\mathrm{2}}\:\:\:\:\left({k}\in\mathbb{Z}\right) \\ $$$${Solution}\:{set} \\ $$$${x}\in\left[\frac{\pi}{\mathrm{4}},\frac{\mathrm{3}\pi}{\mathrm{4}},\frac{\mathrm{5}\pi}{\mathrm{4}},\frac{\mathrm{7}\pi}{\mathrm{4}},\frac{\mathrm{9}\pi}{\mathrm{4}},\frac{\mathrm{11}\pi}{\mathrm{4}}\right] \\ $$$${x}\in\left[\frac{\pi}{\mathrm{2}},\frac{\mathrm{3}\pi}{\mathrm{2}},\frac{\mathrm{5}\pi}{\mathrm{2}}\right] \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *