Question Number 122588 by bramlexs22 last updated on 18/Nov/20
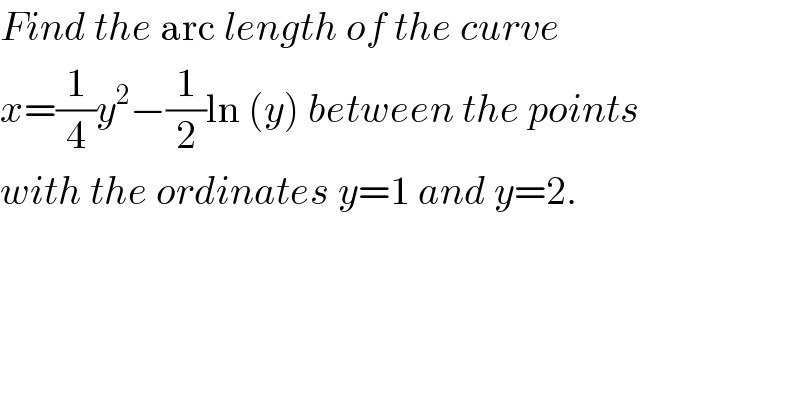
$${Find}\:{the}\:\mathrm{arc}\:{length}\:{of}\:{the}\:{curve}\: \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{4}}{y}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({y}\right)\:{between}\:{the}\:{points} \\ $$$${with}\:{the}\:{ordinates}\:{y}=\mathrm{1}\:{and}\:{y}=\mathrm{2}. \\ $$$$ \\ $$
Answered by MJS_new last updated on 18/Nov/20
![arc length of x=f(y) is given by ∫(√(1+(x′)^2 )) dy x=(1/4)y^2 −(1/2)ln y is defined for y>0 x′=(y/2)−(1/(2y)) (√(1+(x′)^2 ))=(√(((y^2 +1)^2 )/(4y^2 )))=((y^2 +1)/(2y)) [because y>0] ∫((y^2 +1)/(2y))dy=∫(y/2)+(1/(2y))dy=(1/4)y^2 +(1/2)ln y ⇒ arc length is (3/4)+(1/2)ln 2](https://www.tinkutara.com/question/Q122590.png)
$$\mathrm{arc}\:\mathrm{length}\:\mathrm{of}\:{x}={f}\left({y}\right)\:\mathrm{is}\:\mathrm{given}\:\mathrm{by} \\ $$$$\int\sqrt{\mathrm{1}+\left({x}'\right)^{\mathrm{2}} }\:{dy} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{4}}{y}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:{y}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{for}\:{y}>\mathrm{0} \\ $$$${x}'=\frac{{y}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}{y}} \\ $$$$\sqrt{\mathrm{1}+\left({x}'\right)^{\mathrm{2}} }=\sqrt{\frac{\left({y}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}{y}^{\mathrm{2}} }}=\frac{{y}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{y}}\:\left[\mathrm{because}\:{y}>\mathrm{0}\right] \\ $$$$\int\frac{{y}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{y}}{dy}=\int\frac{{y}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}{y}}{dy}=\frac{\mathrm{1}}{\mathrm{4}}{y}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:{y} \\ $$$$\Rightarrow\:\mathrm{arc}\:\mathrm{length}\:\mathrm{is}\:\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mathrm{2} \\ $$
Commented by bramlexs22 last updated on 18/Nov/20
$${thank}\:{you}\:{both}\:{sir} \\ $$
Answered by liberty last updated on 18/Nov/20
![ℓ = ∫_1 ^2 (√(1+(x′)^2 )) dy (dx/dy) = (1/2)y−(1/(2y)) ⇒ℓ=∫_1 ^2 (√(1+((1/2)y−(1/(2y)))^2 )) dy ℓ = ∫_1 ^2 (√(1+(1/4)y^2 +(1/(4y^2 ))−(1/2))) dy ℓ = ∫_1 ^2 (√((1/4)y^2 +(1/2)+(1/(4y^2 )))) dy ℓ = ∫_1 ^2 ((1/2)y+(1/(2y))) dy = [(1/4)y^2 +((ln y)/2) ]_1 ^2 ℓ = (3/4)+((ln 2)/2). ▲](https://www.tinkutara.com/question/Q122591.png)
$$\ell\:=\:\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\:\sqrt{\mathrm{1}+\left(\mathrm{x}'\right)^{\mathrm{2}} }\:\mathrm{dy}\: \\ $$$$\frac{\mathrm{dx}}{\mathrm{dy}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{y}−\frac{\mathrm{1}}{\mathrm{2y}}\:\Rightarrow\ell=\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\:\sqrt{\mathrm{1}+\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{y}−\frac{\mathrm{1}}{\mathrm{2y}}\right)^{\mathrm{2}} }\:\mathrm{dy} \\ $$$$\ell\:=\:\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{y}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4y}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}}\:\mathrm{dy}\: \\ $$$$\ell\:=\:\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\:\sqrt{\frac{\mathrm{1}}{\mathrm{4}}\mathrm{y}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4y}^{\mathrm{2}} }}\:\mathrm{dy}\: \\ $$$$\ell\:=\:\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{y}+\frac{\mathrm{1}}{\mathrm{2y}}\right)\:\mathrm{dy}\:=\:\left[\frac{\mathrm{1}}{\mathrm{4}}\mathrm{y}^{\mathrm{2}} +\frac{\mathrm{ln}\:\mathrm{y}}{\mathrm{2}}\:\right]_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\ell\:=\:\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}.\:\blacktriangle \\ $$
