Question Number 144329 by gsk2684 last updated on 24/Jun/21
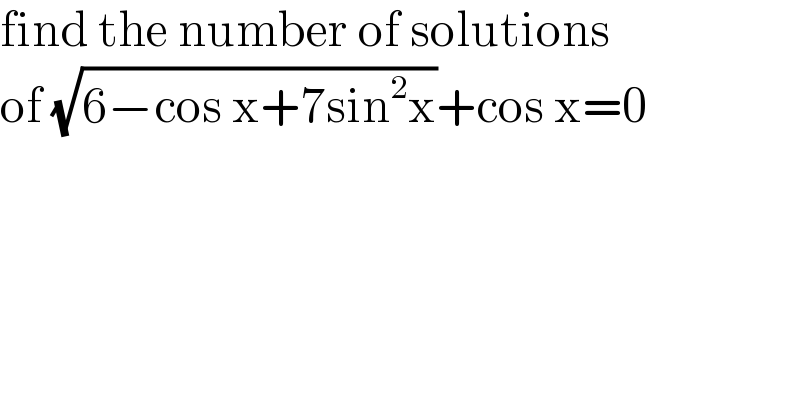
$$\mathrm{find}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{solutions}\: \\ $$$$\mathrm{of}\:\sqrt{\mathrm{6}−\mathrm{cos}\:\mathrm{x}+\mathrm{7sin}^{\mathrm{2}} \mathrm{x}}+\mathrm{cos}\:\mathrm{x}=\mathrm{0} \\ $$
Commented by MJS_new last updated on 25/Jun/21
![let c=cos x ⇒ −1≤c≤1 (√(13−c−7c^2 ))+c=0 ⇒ c<0 (√(13−c−7c^2 ))=−c 13−c−7c^2 =c^2 8c^2 +c−13=0∧c<0 ⇒ c=−((1+(√(417)))/(16))<−1 ⇒ no solution [−1+(√7)≤(√(6−cos x +7sin^2 x))+cos x ≤((−1+2(√(730)))/(14))]](https://www.tinkutara.com/question/Q144375.png)
$$\mathrm{let}\:{c}=\mathrm{cos}\:{x}\:\Rightarrow\:−\mathrm{1}\leqslant{c}\leqslant\mathrm{1} \\ $$$$\sqrt{\mathrm{13}−{c}−\mathrm{7}{c}^{\mathrm{2}} }+{c}=\mathrm{0}\:\Rightarrow\:{c}<\mathrm{0} \\ $$$$\sqrt{\mathrm{13}−{c}−\mathrm{7}{c}^{\mathrm{2}} }=−{c} \\ $$$$\mathrm{13}−{c}−\mathrm{7}{c}^{\mathrm{2}} ={c}^{\mathrm{2}} \\ $$$$\mathrm{8}{c}^{\mathrm{2}} +{c}−\mathrm{13}=\mathrm{0}\wedge{c}<\mathrm{0}\:\:\Rightarrow\:{c}=−\frac{\mathrm{1}+\sqrt{\mathrm{417}}}{\mathrm{16}}<−\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$$$ \\ $$$$\left[−\mathrm{1}+\sqrt{\mathrm{7}}\leqslant\sqrt{\mathrm{6}−\mathrm{cos}\:{x}\:+\mathrm{7sin}^{\mathrm{2}} \:{x}}+\mathrm{cos}\:{x}\:\leqslant\frac{−\mathrm{1}+\mathrm{2}\sqrt{\mathrm{730}}}{\mathrm{14}}\right] \\ $$
Commented by gsk2684 last updated on 25/Jun/21

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{mr}\:\mathrm{MJS} \\ $$
