Question Number 148960 by tabata last updated on 01/Aug/21
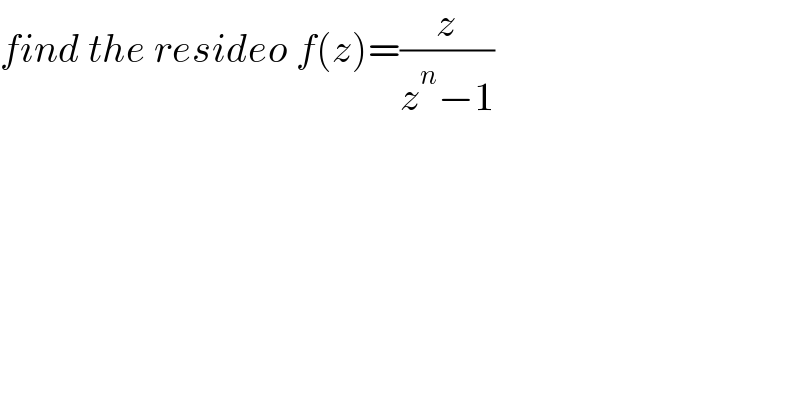
$${find}\:{the}\:{resideo}\:{f}\left({z}\right)=\frac{{z}}{{z}^{{n}} −\mathrm{1}} \\ $$
Answered by mathmax by abdo last updated on 02/Aug/21
![les residus ici sont les poles de f et se sent les racines n^(eme) de lunite cad z_k =e^((i2kπ)/n) and k∈[[0,n−1]] ⇒f(z)=(z/(Π_(k=0) ^(n−1) (z−z_k ))) f(z)=Σ_(k=0) ^∞ (a_k /(z−z_k )) ⇒Res(f,z_k )=a_k =(z_k /(nz_k ^(n−1) )) =(z_k ^2 /n) autre methode f(z)=(z/((z−z_0 )....(z−z_(k−1) )(z−z_k )(z−z_(k+1) )...(z−z_(n−1) )) ⇒Res(f,z_k )=(z_k /((z_k −z_0 )...(z_k −z_(k−1) )(z_k −z_(k+1) )....(z_k −z_(n−1) )))](https://www.tinkutara.com/question/Q148988.png)
$$\mathrm{les}\:\mathrm{residus}\:\mathrm{ici}\:\mathrm{sont}\:\mathrm{les}\:\mathrm{poles}\:\mathrm{de}\:\mathrm{f}\:\:\mathrm{et}\:\mathrm{se}\:\mathrm{sent}\:\mathrm{les}\:\mathrm{racines}\:\mathrm{n}^{\mathrm{eme}} \:\mathrm{de}\:\mathrm{lunite} \\ $$$$\mathrm{cad}\:\:\mathrm{z}_{\mathrm{k}} =\mathrm{e}^{\frac{\mathrm{i2k}\pi}{\mathrm{n}}} \:\mathrm{and}\:\mathrm{k}\in\left[\left[\mathrm{0},\mathrm{n}−\mathrm{1}\right]\right]\:\Rightarrow\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{z}}{\prod_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \left(\mathrm{z}−\mathrm{z}_{\mathrm{k}} \right)} \\ $$$$\mathrm{f}\left(\mathrm{z}\right)=\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{a}_{\mathrm{k}} }{\mathrm{z}−\mathrm{z}_{\mathrm{k}} }\:\Rightarrow\mathrm{Res}\left(\mathrm{f},\mathrm{z}_{\mathrm{k}} \right)=\mathrm{a}_{\mathrm{k}} \:\:=\frac{\mathrm{z}_{\mathrm{k}} }{\mathrm{nz}_{\mathrm{k}} ^{\mathrm{n}−\mathrm{1}} }\:=\frac{\mathrm{z}_{\mathrm{k}} ^{\mathrm{2}} }{\mathrm{n}} \\ $$$$\mathrm{autre}\:\mathrm{methode}\:\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{z}}{\left(\mathrm{z}−\mathrm{z}_{\mathrm{0}} \right)….\left(\mathrm{z}−\mathrm{z}_{\mathrm{k}−\mathrm{1}} \right)\left(\mathrm{z}−\mathrm{z}_{\mathrm{k}} \right)\left(\mathrm{z}−\mathrm{z}_{\mathrm{k}+\mathrm{1}} \right)…\left(\mathrm{z}−\mathrm{z}_{\mathrm{n}−\mathrm{1}} \right.} \\ $$$$\Rightarrow\mathrm{Res}\left(\mathrm{f},\mathrm{z}_{\mathrm{k}} \right)=\frac{\mathrm{z}_{\mathrm{k}} }{\left(\mathrm{z}_{\mathrm{k}} −\mathrm{z}_{\mathrm{0}} \right)…\left(\mathrm{z}_{\mathrm{k}} −\mathrm{z}_{\mathrm{k}−\mathrm{1}} \right)\left(\mathrm{z}_{\mathrm{k}} −\mathrm{z}_{\mathrm{k}+\mathrm{1}} \right)….\left(\mathrm{z}_{\mathrm{k}} −\mathrm{z}_{\mathrm{n}−\mathrm{1}} \right)} \\ $$
