Question Number 26396 by abdo imad last updated on 25/Dec/17
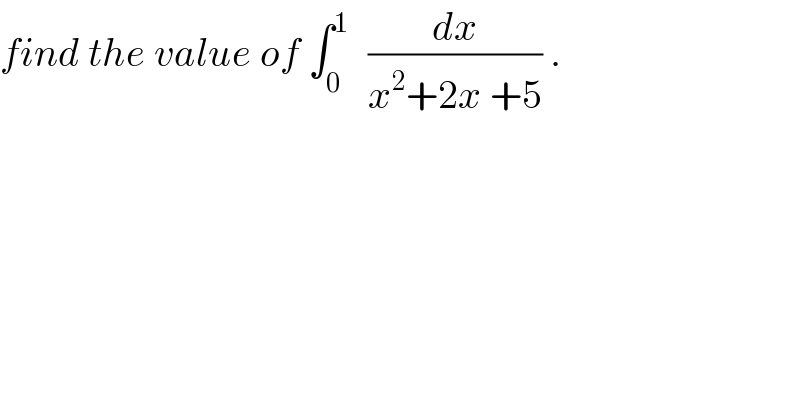
$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\mathrm{1}\:} \:\:\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{2}{x}\:+\mathrm{5}}\:. \\ $$
Commented by abdo imad last updated on 26/Dec/17
![let put I= ∫_0 ^1 (dx/(x^2 +2x+5)) due to x^2 +2x+5=(x+1)^2 +4 we use the changement x+1=2t ⇒ I = ∫_(1/2) ^1 ((2dt)/(4t^2 +4)) = (1/2) ∫_(1/2) ^1 (dt/(1+t^2 )) I=(1/2) [arctant]_(1/2) ^1 = (1/2)(arctan(1)−arctan((1/2))) ⇒ I= (π/8) −(1/2)arctan((1/2))](https://www.tinkutara.com/question/Q26579.png)
$${let}\:{put}\:{I}=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5}}\:\:{due}\:{to}\:\:{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5}=\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}\:{we}\:{use}\: \\ $$$${the}\:{changement}\:{x}+\mathrm{1}=\mathrm{2}{t}\:\:\Rightarrow\:\:\:{I}\:\:=\:\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{2}{dt}}{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{4}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\:\left[{arctant}\right]_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} =\:\frac{\mathrm{1}}{\mathrm{2}}\left({arctan}\left(\mathrm{1}\right)−{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$\Rightarrow\:\:\:{I}=\:\:\:\frac{\pi}{\mathrm{8}}\:\:−\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$
Answered by jota@ last updated on 25/Dec/17
![∫_0 ^1 ((d(x+1))/((x+1)^2 +2^2 ))=(1/2)tan^(−1) (((x+1)/2))∣_0 ^1 =(1/2)[tan^(−1) 1−tan^(−1) (1/2)].](https://www.tinkutara.com/question/Q26404.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{d}\left({x}+\mathrm{1}\right)}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}+\mathrm{1}}{\mathrm{2}}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{tan}^{−\mathrm{1}} \mathrm{1}−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{1}/\mathrm{2}\right)\right]. \\ $$
