Question Number 38651 by rahul 19 last updated on 28/Jun/18
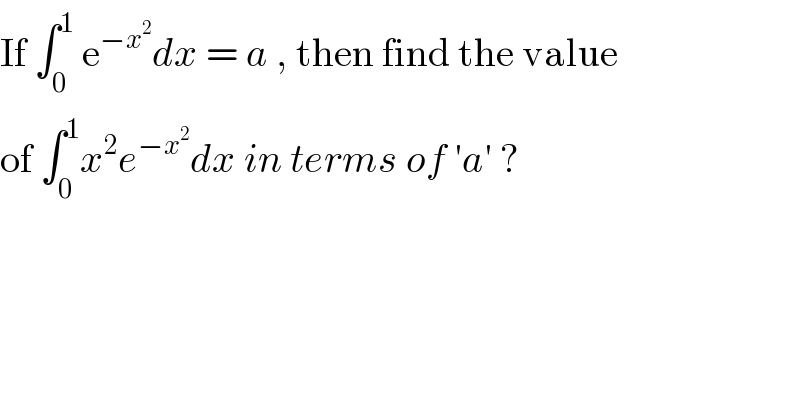
$$\mathrm{If}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{e}^{−{x}^{\mathrm{2}} } {dx}\:=\:{a}\:,\:\mathrm{then}\:\mathrm{find}\:\mathrm{the}\:\mathrm{value} \\ $$$$\mathrm{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} } {dx}\:{in}\:{terms}\:{of}\:'{a}'\:? \\ $$
Answered by MrW3 last updated on 28/Jun/18
![∫_0 ^1 x^2 e^(−x^2 ) dx =−(1/2)∫_0 ^1 xde^(−x^2 ) =−(1/2)[xe^(−x^2 ) −∫_0 ^1 e^(−x^2 ) dx]_0 ^1 =−(1/2)[xe^(−x^2 ) ]_0 ^1 +(1/2)∫_0 ^1 e^(−x^2 ) dx =−(1/(2e))+(a/2) =(1/2)(a−(1/e))](https://www.tinkutara.com/question/Q38665.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} } {dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {xde}^{−{x}^{\mathrm{2}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left[{xe}^{−{x}^{\mathrm{2}} } −\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{−{x}^{\mathrm{2}} } {dx}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left[{xe}^{−{x}^{\mathrm{2}} } \right]_{\mathrm{0}} ^{\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{−{x}^{\mathrm{2}} } {dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}{e}}+\frac{{a}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({a}−\frac{\mathrm{1}}{{e}}\right) \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 28/Jun/18

$${excellent}… \\ $$
Commented by rahul 19 last updated on 28/Jun/18

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}! \\ $$
