Question Number 114152 by mohammad17 last updated on 17/Sep/20
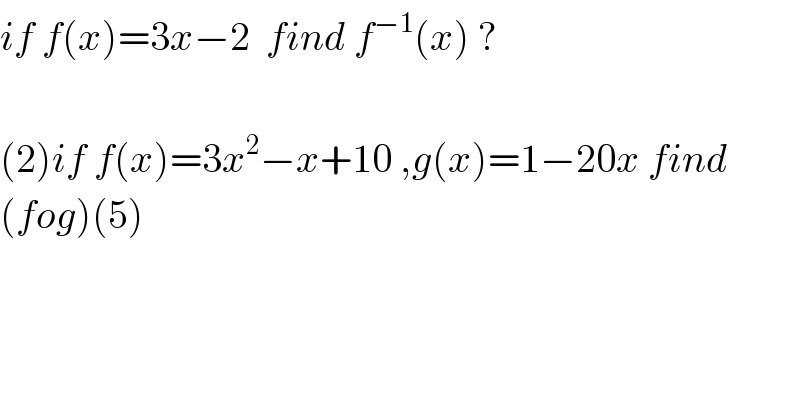
$${if}\:{f}\left({x}\right)=\mathrm{3}{x}−\mathrm{2}\:\:{find}\:{f}^{−\mathrm{1}} \left({x}\right)\:? \\ $$$$ \\ $$$$\left(\mathrm{2}\right){if}\:{f}\left({x}\right)=\mathrm{3}{x}^{\mathrm{2}} −{x}+\mathrm{10}\:,{g}\left({x}\right)=\mathrm{1}−\mathrm{20}{x}\:{find}\: \\ $$$$\left({fog}\right)\left(\mathrm{5}\right) \\ $$
Answered by bemath last updated on 17/Sep/20
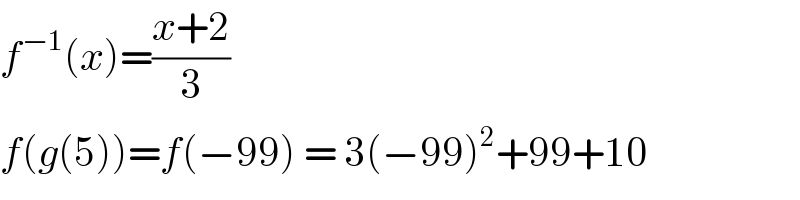
$${f}^{−\mathrm{1}} \left({x}\right)=\frac{{x}+\mathrm{2}}{\mathrm{3}} \\ $$$${f}\left({g}\left(\mathrm{5}\right)\right)={f}\left(−\mathrm{99}\right)\:=\:\mathrm{3}\left(−\mathrm{99}\right)^{\mathrm{2}} +\mathrm{99}+\mathrm{10} \\ $$
Commented by mohammad17 last updated on 17/Sep/20

$${thank}\:{you}\:{sir} \\ $$
Answered by physicstutes last updated on 17/Sep/20
![(1) f(x) = 3x−2 let f(x) = u ⇒ u = 3x−2 u + 2 = 3x and x = ((u+2)/3) ∴ f^(−1) (x) = ((x + 2)/3). (2) f(x) = 3x^2 −x + 10 and g(x) = 1−20 x f_o g (5)= f[g(5)] but g(5) = 1−20(5) = 1−100 = −99. ⇒ f_o g(5) = f(−99) and f(−99) = 3(−99)^2 −(−99) + 10 = 3(970,299) + 99 + 10 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− (1) f^(−1) (x) = ((x + 2)/3) , (2) f _o g (5) = 2,910, 997](https://www.tinkutara.com/question/Q114198.png)
$$\left(\mathrm{1}\right)\:{f}\left({x}\right)\:=\:\mathrm{3}{x}−\mathrm{2} \\ $$$$\mathrm{let}\:{f}\left({x}\right)\:=\:{u} \\ $$$$\Rightarrow\:{u}\:=\:\mathrm{3}{x}−\mathrm{2}\: \\ $$$$\:{u}\:+\:\mathrm{2}\:=\:\mathrm{3}{x} \\ $$$$\mathrm{and}\:\:{x}\:=\:\frac{{u}+\mathrm{2}}{\mathrm{3}} \\ $$$$\therefore\:{f}^{−\mathrm{1}} \left({x}\right)\:=\:\frac{{x}\:+\:\mathrm{2}}{\mathrm{3}}. \\ $$$$\left(\mathrm{2}\right)\:{f}\left({x}\right)\:=\:\mathrm{3}{x}^{\mathrm{2}} −{x}\:+\:\mathrm{10}\:\mathrm{and}\:\mathrm{g}\left({x}\right)\:=\:\mathrm{1}−\mathrm{20}\:{x} \\ $$$$\:{f}_{{o}} \:\mathrm{g}\:\left(\mathrm{5}\right)=\:{f}\left[\mathrm{g}\left(\mathrm{5}\right)\right] \\ $$$$\mathrm{but}\:\mathrm{g}\left(\mathrm{5}\right)\:=\:\mathrm{1}−\mathrm{20}\left(\mathrm{5}\right)\:=\:\mathrm{1}−\mathrm{100}\:=\:−\mathrm{99}. \\ $$$$\:\Rightarrow\:{f}_{{o}} \mathrm{g}\left(\mathrm{5}\right)\:=\:{f}\left(−\mathrm{99}\right)\: \\ $$$$\:\mathrm{and}\:{f}\left(−\mathrm{99}\right)\:=\:\mathrm{3}\left(−\mathrm{99}\right)^{\mathrm{2}} −\left(−\mathrm{99}\right)\:+\:\mathrm{10}\:=\:\mathrm{3}\left(\mathrm{970},\mathrm{299}\right)\:+\:\mathrm{99}\:+\:\mathrm{10} \\ $$$$\:−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$$\left(\mathrm{1}\right)\:{f}^{−\mathrm{1}} \left({x}\right)\:=\:\frac{{x}\:+\:\mathrm{2}}{\mathrm{3}}\:,\:\left(\mathrm{2}\right)\:\:\:{f}\:_{{o}} \:\mathrm{g}\:\left(\mathrm{5}\right)\:=\:\mathrm{2},\mathrm{910},\:\mathrm{997} \\ $$
