if-y-z-x-10-3-and-x-z-3-4-find-x-y-

Question Number 150792 by mathdanisur last updated on 15/Aug/21

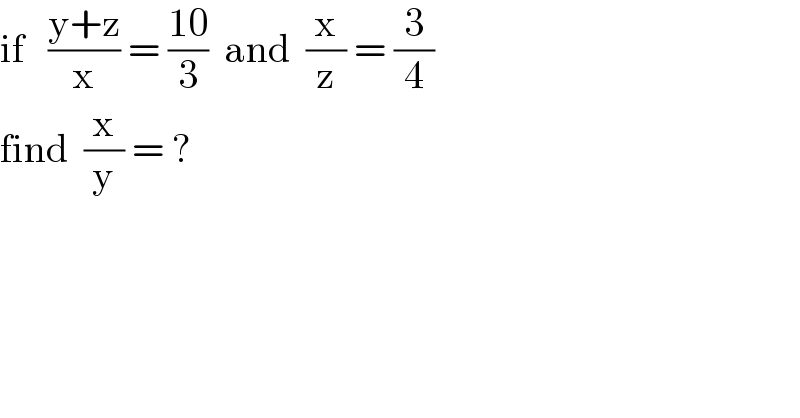
$$\mathrm{if}\:\:\:\frac{\mathrm{y}+\mathrm{z}}{\mathrm{x}}\:=\:\frac{\mathrm{10}}{\mathrm{3}}\:\:\mathrm{and}\:\:\frac{\mathrm{x}}{\mathrm{z}}\:=\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{find}\:\:\frac{\mathrm{x}}{\mathrm{y}}\:=\:? \\ $$

Answered by nimnim last updated on 15/Aug/21

$${y}=\frac{\mathrm{10}{x}−\mathrm{3}{z}}{\mathrm{3}}\:\:\:\:{and}\:\:\:\:\mathrm{3}{z}=\mathrm{4}{x} \\ $$$$\therefore\frac{{x}}{{y}}=\frac{{x}}{\frac{\mathrm{10}{x}−\mathrm{4}{x}}{\mathrm{3}}}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by mathdanisur last updated on 15/Aug/21

$$\mathrm{Thankyou}\:\mathrm{Ser} \\ $$

Answered by Rasheed.Sindhi last updated on 15/Aug/21

$$\:\:\:\:\frac{\mathrm{y}+\mathrm{z}}{\mathrm{x}}\:=\:\frac{\mathrm{10}}{\mathrm{3}}\:\:\mathrm{and}\:\:\frac{\mathrm{x}}{\mathrm{z}}\:=\:\frac{\mathrm{3}}{\mathrm{4}};\frac{\mathrm{x}}{\mathrm{y}}\:=\:? \\ $$$$\frac{\mathrm{y}}{\mathrm{x}}+\frac{\mathrm{z}}{\mathrm{x}}=\frac{\mathrm{10}}{\mathrm{3}}\:\: \\ $$$$\frac{\mathrm{y}}{\mathrm{x}}+\frac{\mathrm{4}}{\mathrm{3}}=\frac{\mathrm{10}}{\mathrm{3}}\:\:\left[\:\because\:\frac{\mathrm{x}}{\mathrm{z}}\:=\:\frac{\mathrm{3}}{\mathrm{4}}\Rightarrow\frac{\mathrm{z}}{\mathrm{x}}=\frac{\mathrm{4}}{\mathrm{3}}\right] \\ $$$$\frac{\mathrm{y}}{\mathrm{x}}=\frac{\mathrm{10}}{\mathrm{3}}−\frac{\mathrm{4}}{\mathrm{3}}=\frac{\mathrm{6}}{\mathrm{3}}=\mathrm{2} \\ $$$$\frac{\mathrm{x}}{\mathrm{y}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by mathdanisur last updated on 15/Aug/21

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$

Answered by maged last updated on 15/Aug/21

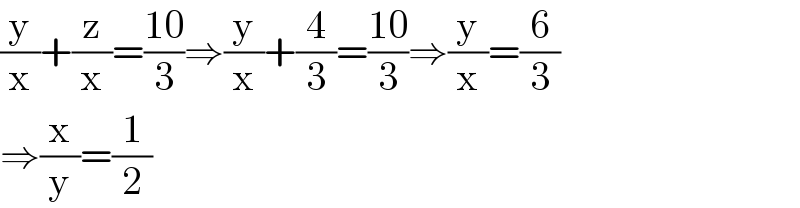
$$\frac{\mathrm{y}}{\mathrm{x}}+\frac{\mathrm{z}}{\mathrm{x}}=\frac{\mathrm{10}}{\mathrm{3}}\Rightarrow\frac{\mathrm{y}}{\mathrm{x}}+\frac{\mathrm{4}}{\mathrm{3}}=\frac{\mathrm{10}}{\mathrm{3}}\Rightarrow\frac{\mathrm{y}}{\mathrm{x}}=\frac{\mathrm{6}}{\mathrm{3}} \\ $$$$\Rightarrow\frac{\mathrm{x}}{\mathrm{y}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com