Question Number 43874 by peter frank last updated on 16/Sep/18
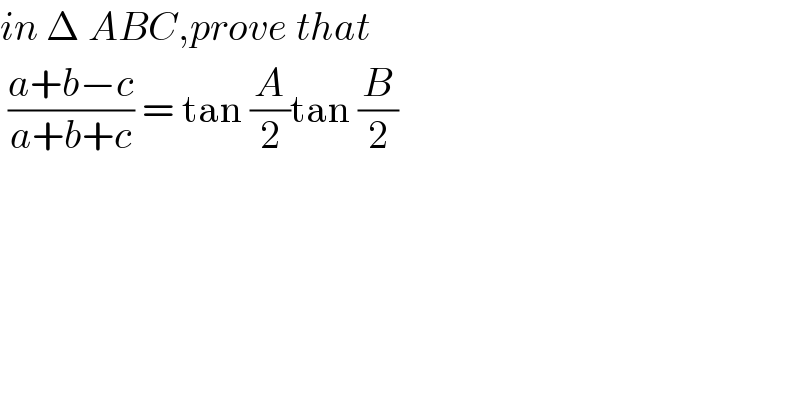
$${in}\:\Delta\:{ABC},{prove}\:{that} \\ $$$$\:\frac{{a}+{b}−{c}}{{a}+{b}+{c}}\:=\:\mathrm{tan}\:\frac{{A}}{\mathrm{2}}\mathrm{tan}\:\frac{{B}}{\mathrm{2}}\: \\ $$
Answered by ajfour last updated on 16/Sep/18
![((a+b−c)/(a+b+c))=((sin A+sin B−sin (A+B))/(sin A+sin B+sin (A+B))) = ((2sin (((A+B)/2))[cos (((A−B)/2))−cos (((A+B)/2))])/(2sin (((A+B)/2))[cos (((A−B)/2))+cos (((A+B)/2))])) = ((2sin (A/2)sin (B/2))/(2cos (A/2)cos (B/2))) = tan (A/2)tan (B/2) .](https://www.tinkutara.com/question/Q43879.png)
$$\frac{{a}+{b}−{c}}{{a}+{b}+{c}}=\frac{\mathrm{sin}\:{A}+\mathrm{sin}\:{B}−\mathrm{sin}\:\left({A}+{B}\right)}{\mathrm{sin}\:{A}+\mathrm{sin}\:{B}+\mathrm{sin}\:\left({A}+{B}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{2sin}\:\left(\frac{{A}+{B}}{\mathrm{2}}\right)\left[\mathrm{cos}\:\left(\frac{{A}−{B}}{\mathrm{2}}\right)−\mathrm{cos}\:\left(\frac{{A}+{B}}{\mathrm{2}}\right)\right]}{\mathrm{2sin}\:\left(\frac{{A}+{B}}{\mathrm{2}}\right)\left[\mathrm{cos}\:\left(\frac{{A}−{B}}{\mathrm{2}}\right)+\mathrm{cos}\:\left(\frac{{A}+{B}}{\mathrm{2}}\right)\right]} \\ $$$$\:\:\:\:\:\:\:=\:\frac{\mathrm{2sin}\:\frac{{A}}{\mathrm{2}}\mathrm{sin}\:\frac{{B}}{\mathrm{2}}}{\mathrm{2cos}\:\frac{{A}}{\mathrm{2}}\mathrm{cos}\:\frac{{B}}{\mathrm{2}}}\:=\:\mathrm{tan}\:\frac{{A}}{\mathrm{2}}\mathrm{tan}\:\frac{{B}}{\mathrm{2}}\:. \\ $$
Commented by peter frank last updated on 17/Sep/18

$${thank}\:{you} \\ $$$$ \\ $$
